|
The Evenden-Brunner-Inversion. Only a small program in my map projection colletion but an importing closing of a an painful gap in map projection theory.
The common map projection formulas transformes the spheric Earth surface coodinates longitude λ and latitude φ into the map coordinates x and y (direct transformation). But often inverse formulas are needed to transform a map-x,y-pair into λ and φ.
The Winkel Tripel of Oswald Winkel 1913 is one of the most popular map projections. But it is not invertable in a closed analytical form. And it is not a running implementation known.
Cengizhan Ipbüker/I. Öztug Bildirici have publicated in 2002 (see below) a Winkel-Tripel-Inversion method in theory. G. I. Evenden gives in Issue 2008 Libroj.4 manual a Aïtoff inversion solution. Jakob Brunner, Luzern has me sent a Winkel Inversion Excel solution by means of Newton-Raphson-Iteration.
With best regards to Jakob Brunner, Luzern.
Test run #1 - First implementation test
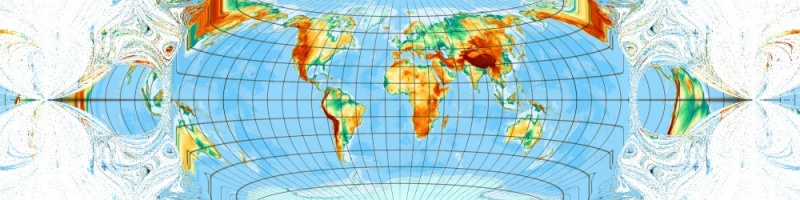
Brunners original initial point arc 1/1 (alias 57/57 degree, near Perm, Russia). One iteration gives a linear approimation ...
2 iterations - quadratic approximation ...
3 iterations, cubic solution ...
5 iterations -
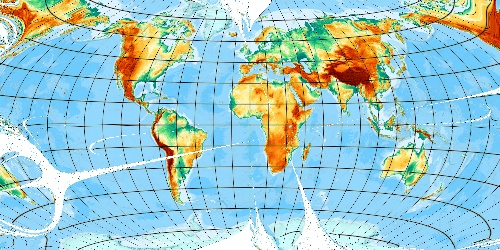
10 iterations -
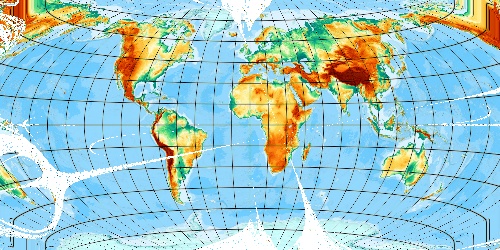
Okay - it runs and may become a Winkel Tripel. But it is still some to do ...
Test run #2 - New convergence raw
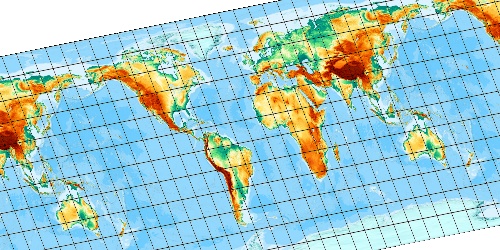
We take initial point 1 degree E 1 degree N. Linear ...
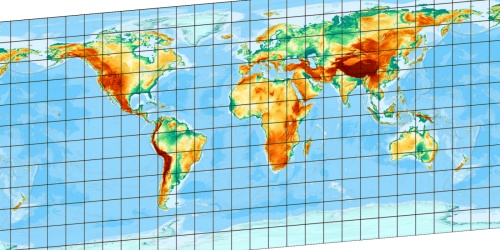
Quadratic ...
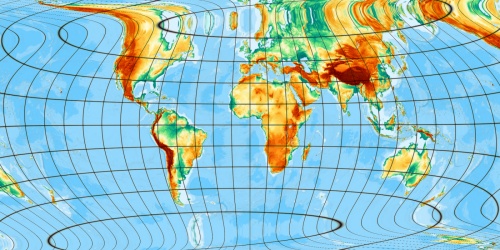
Cubic ...
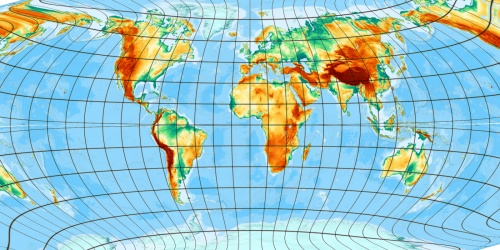
But higher appoximations, here 5 gives a bad divergence gap on outer equatorial areas.
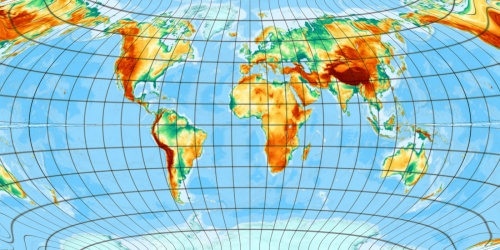
10 cycles:
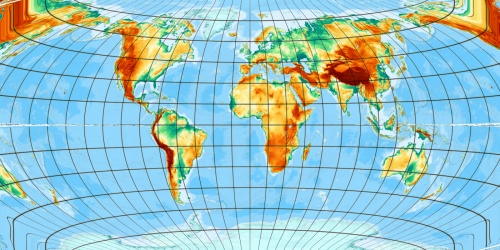
20 cycles.
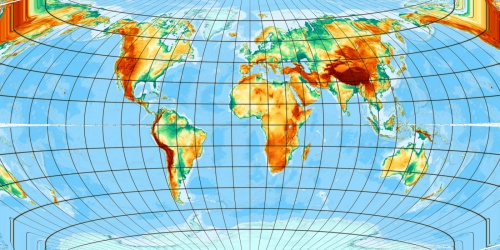
OK, it is a Winkel Tripel. But note the visible gap at outer (far east and west) equator. That's a problem. Also a (more academic) problem is the assymetry caused by the 1 E 1 N located inital point - near the image centre but outside of any symmetry axis.
Test run #3 - Iteration step analysis ...
More deeper analyzing. We change algorithm and indicator. We take a epsilon value as precision target and count and write the needed steps as grey value in each pixel. Black means bad convergence (>15 iteration steps), lighter and more lighter grey a rising better convergence. The numbers are the numbers of iteration steps to reach the epsilon accuracy ...
What is the influence of epsilon? Epsilon=0.000000001 („convergence class e-09“) is Brunners original value.
Initial point in that row is is E 180 N 0. It gives good solutions near the equator but near the poles are needed 20 ... 30 iterations.
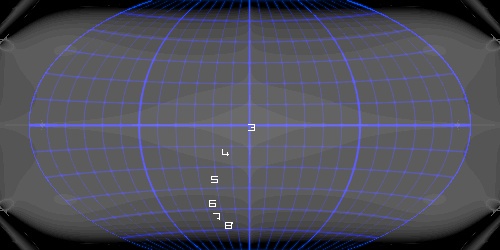
A lower epsilon=0.0000001 („convergence class e-07“) gives a larger convergence area ...
Here epsilon=0.00001 ...
Greather epsilons cause less iteration steps and a faster computation but a lower precision. The epsilon of 0.00000001 ist optimal. It also is the by Brunner recommended value.
Test run #4 - Some interesting images
Now a further search for initial points. As temporary work epsilon we use 0.0001 (ce-05) ...
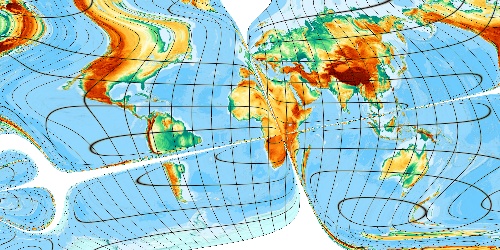
Full central initialisation at 0 E 0 N shows a bad solution. We see the „latitude-45-degree-limitation“:
Initialization point 45 E 45 N (near brunners 57/57 „natural arc“ perm point) gives convergence images similar above in test run #1 ...
At a coffee break: Start point 85 E 90 N gives a very smart design ...
Test run #5 - Systematical search along equator
Now a systematic search for an intial point along the equator. We know from test run #3: 180 E 0 N gives a good convergence - except near the poles.
We shift the initial point along the equator inside the map centre, 135 E 0 N ...
90 E 0 N ...
45 E 0 N ...
No better convergence near the poles.
0 E 0 N - thats the image wirth the „latitude-45-degree-limitation“ ...
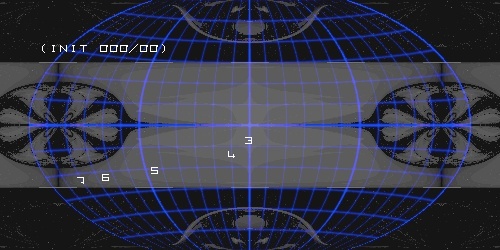
Better solutions but still suboptimal.
Test run #6 - Systematical search along greenwich meridian
Now a search for the initial point along the central meridian.
North pole initialization gives large (black) fractal gaps arround the equator in far east and far west ...
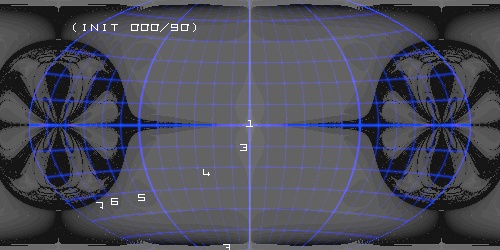
0 E 75 N ... decreasing latitude gives smaller gaps ...
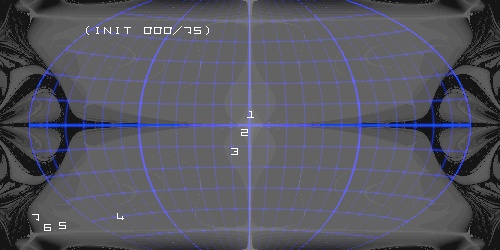
0 E 45 N ... better, but still bad convergence on outer equator ...
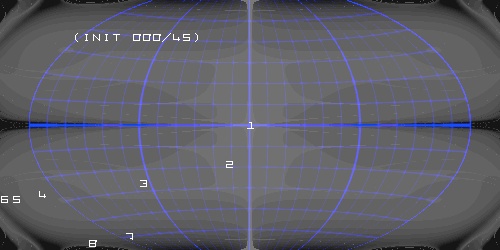
But I'm angry. At 0 E 0 N will come the „latitude-45-degree-limitation“. We take 5 N 0 E ...
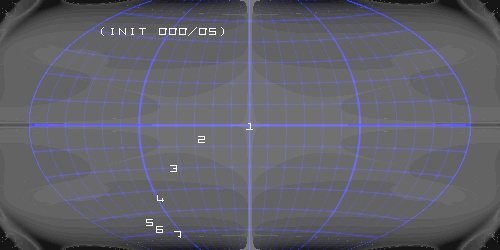
... okay ... and now 0 E 1 N ...
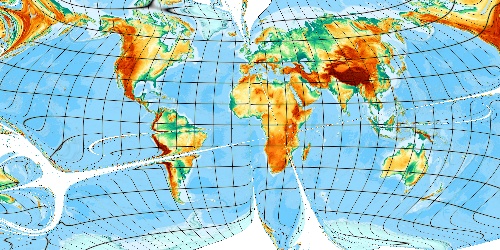
We risk further decreasing very near to the equator, 0 E 0.0625 degree N:
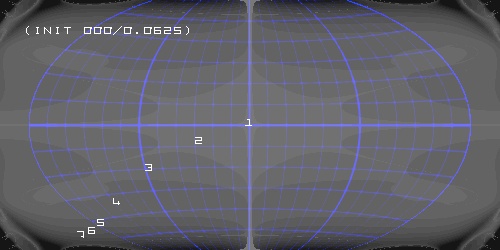
Very good! We note 0 E 0.062570 N as best result.
At end of this raw initial point 0 N 0 E (equator) gives the known image with the „latitude-45-degree-limitation“:
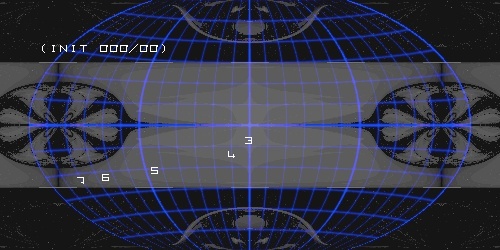
0 E 0.0625 is found as the best initial point!
Okay, it runs. And now the Release runs ...
Test run #7 - A very large codomain map
We have found good convergence conditions: initial point latitude 0.0625 degree, longitude 0 degree, epsilon 1E-09. To demonstrate it, we compute a „very large codomain map“, half default scale, 1:600.000.000 ...
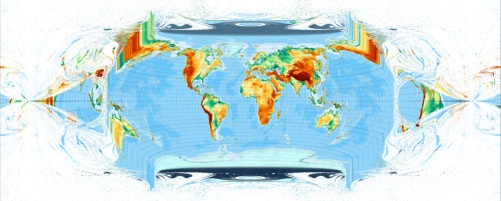
It shows: Latitudes > 90 and longitudes > 180 also often gives a practicable results. It is possible to compute pixel outside pole and date line. OK, there is no need for outside pole pixels, but to compute outside date line pixel - that can make sense.
Large codomain map 1:400.000.000 (944 kByte)
The Release run
It runs and now - the release map ...
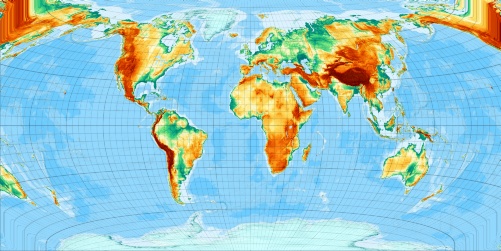
Large image 1:400.000.000 (188 kByte)
Large image 1:200.000.000 (931 kByte)
Here a compasision with direct generation:
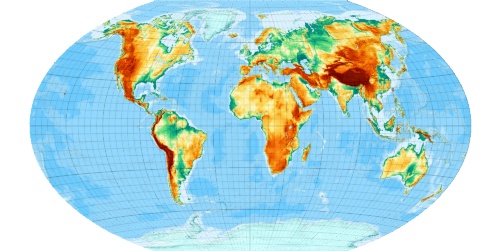
It is the same map. But note: a function and its inverse change their codomain and image. The inverse runs all over the map and the Evenden-Brunner-Interation also gives a solution outside the date line.
Literature:
Cengizhan Ipbüker, I. Öztug Bildirici, 2002: A General Algorithm fot the Inverse Transformation of Map Projections Using Jacobian Matrices Proceedings of the Third International Symposium Mathematical & Computational Applications September 4-6, 2002. Konya, Turkey, pp. 175-182 [Insbesondere mit einer Winkel Tripel Inversion.] http://atlas.selcuk.edu.tr/paperdb/papers/130.pdf
Böhm, R.: Variationen von Weltkartennetzen der Wagner-Hammer-Aïtoff-Entwurfsfamilie. Kartographische Nachrichten 56. Jg., Nr. 1., p. 8-16. - Kirschbaum: Bonn 2006.
Brunner, Jakob, Luzern 1020: Mail Correspondence.
Canters, F., 2002: Small-scale Map Projection Design (p. 185). London: Taylor & Francis 2002.
Evenden, G.I., 2008: Issue 2008 Libproj.4 manual
Grafarend, Erik, Krumm, Friedrich W., 2006: Map Projections. Berlin: Springer 2006.
Wagner, K.: Kartographische Netzentwürfe. Leipzig: Bibliographisches Instuitut 1949.