Back Ground: The Natural Equivalence of Areal and Angular Distortion
Die Lösung von Bernhard Jennys Aufgabe
Ein Kartennetzentwurf kann niemals die Erde ohne Verzerrungen in die Ebene abbilden. Man kann allerdings die Abbildung so wählen, dass entweder alle Winkel oder alle Flächen richtig abgebildet werden. Die Karte kann also entweder winkeltreu oder flächentreu sein. Winkeltreue und Flächentreue sind gleichsam fundamentale theoretische „Eigenschaftspole“ der gesamten Kartennetzentwurfslehre.
Okay, praktisch also die Mitte zwischen winkel- und flächentreuen Netzen wählen? Keine schlechte Idee, die zu den sog. „vermittelnden“ Kartennetzentwürfen führt. Die Theorie hat damit freilich ein kleines Problem, das nach meinem Kenntnisstand ungelöst ist, nämlich: Wie kann einer Flächenabweichung ein bestimmter Winkelfehler als „gleichgroß“ zugeordnet werden? Schwierig, Äpfel sind nicht Birnen und Flächen lassen sich nun mal nicht in Winkel umrechnen. Der aktuelle Kenntnisstand kommt aus der empirischen Kartographie (W. G. Koch), man lässt verschiedene Karten von Kartennutzern bewerten. Wenn dann „67,9 %“ aller Testprobanden meinen, dass Musterkarten mit „173 %“ Flächenverzerrung „genauso gut“ aussehen, wie Vergleichskarten mit „38,7°“ Winkelfehler, kann dies ein gewisser Anhalt für den Kartenredakteur sein. Sowas ist natürlich sehr spekulativ. Den Mathematiker wird sowas nicht befriedigen.
Wie könnte man es besser machen?
Verzerrungen können analysiert werden. Im Kern der Projektionsanalyse malt man die gesamte Oberfläche unserer Erdkugel mit „differentiell kleinen“ Kreisen voll, Radiusannahme üblicherweise „1“. Die Kugel wird dann in die Kartenebene projiziert. Aus den Kreisen werden so Ellipsen – das sind die berühmten Tissotellipsen. Die haben jeweils zwei Halbachsen, a und b. Bei a = b sind die Tissotellipsen auch wieder Kreise. Dann ist unsere Abbildung (in dem betreffenden Punkt) winkeltreu. Wenn a multipliziert mit b exakt 1 ergibt, so haben die Tissotellipsen dieselbe Fläche wie die Urbildkreise. Der Punkt wurde flächentreu abgebildet.
Der Kerngedanke ist nun, das sich die Tissotellipsen-Halbachsen a und b in Flächen- und Winkelverzerrungen umrechnen lassen, die Formeln hierzu sind bekannt (z. B. Wagner, S. 13, S. 26; Swonarew, S. 29ff.). Die Flächenverzerrung S ermittelt man mit:
S = a × b
Für die Winkelverzerrung nehmen wir den Wert der Richtung der größten Verzerrung – das ist zugleich die Hälfte der maximalen Winkelverzerrung – ω an:
ω = arcsin((a-b)/(a+b))
Weitere Vorgehensweise nun wie folgt: Man wähle für eine hypothetische große Halbachse einer Tissotellipse einen beliebigen Wert a ungleich 1. Als kleine Halbachse b wähle man das Reziproke von a, 1/a. Mit diesen beiden Werten können nun drei Tissotellipsen T1, T2 und T3 wie folgt konstruiert werden: T1 mit beiden Halbachsen der Länge a. T2 habe die Halbachsen a und b. Bei T3 haben beide Halbachsen die Länge b. T1 ist ein Kreis und indiziert folglich eine winkeltreue Abbildung. T2 steht mit a×b=1 für Flächentreue. T3 ist das „akademische Geschwisterkind“ von T1 und wie T1 anzusehen. Nun werde ein Punkt durch zwei hypothetische Kartennetzentwürfe abgebildet, der eine sei winkeltreu, der andere sei flächentreu. Wir bewerten dann beide Entwürfe als gleichstark verzerrt, wenn dieser Tissotellipse T1 und jener Tissotellipse T2 erzeugt. Das bezeichne ich als natürliche Äquivalenz von Winkel- und Flächenverzerrung auf Grundlage der Tissotellipse.
Indem man das mit einzelnen Werten durchrechnet, erhält man konkrete Beträge für Winkel- und Flächenfehler:
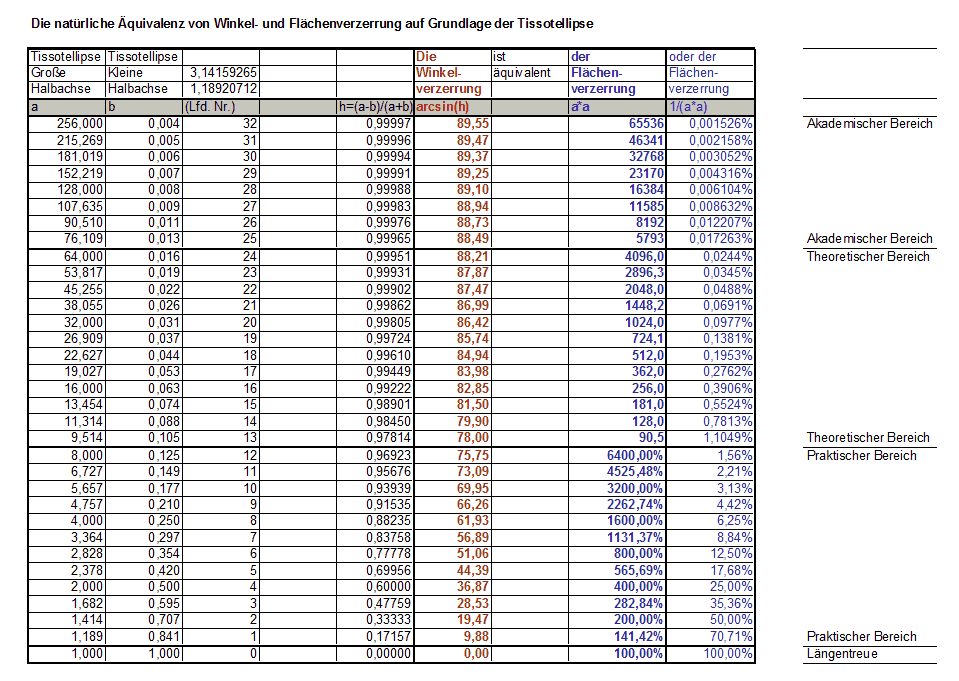
Wie man sieht, entspricht eine Flächenverzerrung von 400 % einer Winkelverzerrung von 36,87°. Bei einer Längenverzerrung auf das Achtfache entstehen 64fach vergrößerte Flächen. Das entspricht einer Winkelverzerrung von 75,75°. Das ist zugleich eine ungefähre Grenze, die der Praktiker nicht überschreiten sollte. Jenseits von 6400 % Fläche und 75 ° Winkelverzerrungen beginnt der Bereich der nur noch für Theoretiker interessant ist. Und nahe 90° wird es dann ganz akademisch, hier beginnt der Bereich der Abbildung der Erdoberfläche auf einen Bindfaden.
Zu den benutzten Formeln siehe die Excel-Datei, mit der die Tabelle erstellt wurde.
Ich bedanke mich bei Bernhard Jenny, ETH Zürich für die Anregung zu diesen Überlegungen. Jenny suchte bei der Implementierung seines Flex Projectors nach einem Wert, der als „globale“ Verzerrungsschranke geeignet ist. Aus der Literatur (z. B. Bugayevskiy/Snyder 1998) bekannte Kriterien, wie z. B. die Kriterien nach Airy, Airy-Kavrayskiy, Jordan, Klingach, Konusova etc. lehnt er ab, weil diese doch sehr speziell sind. Flächenverzerrung und Winkelverzerrung wären da viel anschaulicher ... so folgte er einer Anregung Čapeks ... wenn man sie nur auf ein gemeinsames Maß bringen könnte ...
Ich bedanke mich bei Jannis Kaiser, Mainz für die Anregung zu einer Überarbeitung der Seite 2017. Jenny ist zuzustimmen, dass „globale Kriterien“ im Lokalen versagen, Canters ist zuzustimmen, dass „lokale Verzerrungsmaße im Großen versagen“. Die Sache ist ungelöst und darum ist so „Patent-Besten-Netzentwürfen-Der-Welt“ wie Peterprojektion oder Narukawa analytisch schlecht etwas entgegenzusetzen.
25.08.2017 Überarbeitet