Du und deine Reihenentwicklung
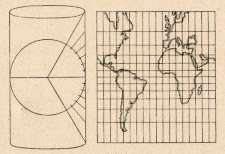[Abbildung: Wagner S. 33]
Die Königin der Kartennetzentwürfe
Die Königin der Kartennetzentwürfe ist die Gauß-Krüger-Projektion. Immer wenn in unseren Garmins etwas mit UTM, WGS84, ED50, Besselellipsoid, Krassowski, Streifennummer, Hochwert, Grad, Minuten und Sekunden nicht hinhaut — ja Kinder, dann muss man eben so fix einmal eine Gauß-Krüger-Projektion rechnen. Aber kaum ein Mensch — außer Winfried Korth in Potsdam und Friedrich Krumm in Stuttgart — (die ich beide sehr verehre) wissen, was sich dahinter verbirgt.
Die Gauß-Krüger-Projektion ist nicht von Kartographen, sondern von Geödaten gemacht worden, worunter wir mal den alten Gauß subsummieren wollen. Das bedeutet, dass man statt mit überschaubaren Formeln zu arbeiten, schlagartig einen aus resperkteinflößenden elliptischen Integralen erster Art bestehenden Pulverdampfnebel braut.
Der entscheidende Trick ist, man darf in der Wikipedia nicht unter Gauß-Krüger-Projektion nachgucken, sondern muss das Stichwort Meridianbogen wählen. Dort haben wir dan schon den ollen Delambre von 1799.
Willkommen in der herrlichen Welt der Reienentwickungen
sondern ein Ellipsoid, es aber C) aber, letztendlich &alles Das sieht auf den ersten Blick nicht allzu innovativ aus, dennoch sind diese Netze für gewisse Spezialzwecke durchaus brauchbar, insbesondere wenn flächenproportionale zonale Erscheinungen darzustellen sind.
Quelle hier meist G. I. Evenden: Libproj4 Preliminary Draft, March 2005, 4.1.3
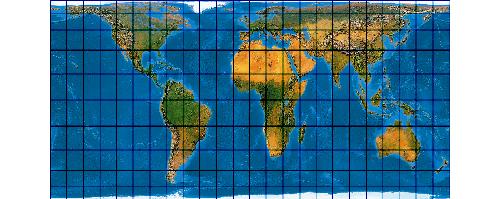
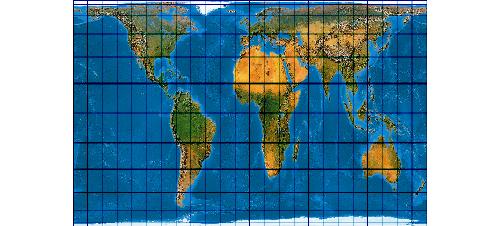
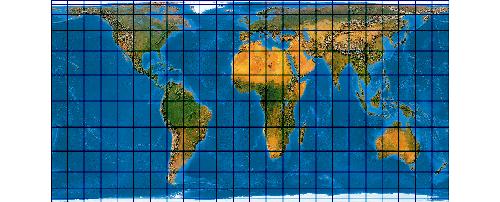
Was die Emser Depesche für das 19.Jahrhundert war, ist die Peters-Projektion für das Jahr 1974. Da hat nämlich ein „Professor Arno Peters“ seinem eigenen Bekunden zufolge eine Art perpetuum mobile der Kartographie erfunden.
Über dieses Meisterstück der Weltkartenreklame liegen im Internet rum, unbedingt hier draufklicken, das ist der Reinhold Pfarrpfeiffer der Kartographie!
Auf so einen Fake muss erst einmal einer kommen. Der Troll, Mensch, Klasse der schreibt dass die Peters-Karten so schön rechteckig sind und der Äquator in der Mitte. Und die Breitenkreise gehen so schön quer rüber und die Längenkreise runterzu.
Blos die tüteligen Kartographieprofessoren Canters & Decleir haben das noch nicht begriffen und schreiben bierernst (The World in Perspective, 1989, S. 161): The projection is completely unsuitable for general purpose world maps because of the extreme scale distortions.
(Extreme scale distortions - was ist das denn nun wieder für ein Zeugs? Kann man das in der Mikrowelle warm machen?)
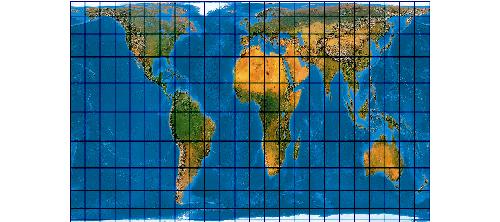
Der Clou ist auch, dass die Formel irgendjemand mal falsch abgeschrieben hat. Und nun haben wir einen Peters nach Voxland und einen Peters nach Mailing.
Macht nichts - wir wissen ja, man kann für den flächentreuen Schnittzylinder im Prinzip jeden beliebigen Schnittparallel von 0 bis 90 Grad auswürfeln. Um den Schnittparallel herum stimmt es einigermaßen, weiter weg wird es immer verzerrter.
(Was mir da noch einfällt - hat der Peters da nicht immer betont, dass gerade sein Netz die Supereigenschaft hätte, unser „falsches“ „europazentriertes“ Weltbild zu korrigieren und eher Afrika oder Südamerika endlich „richtig“ darzustellen? Blos - um Afrika einigermaßen verzerrungsarm darzustellen, dazu müsste doch der Schnittparallel ungefähr durch Afrika gehen? Die etwa 45 ° liegen aber nun in Norditalien, Venedig, etwa. Na ... vielleicht ... klar ... Venedig liegt ja aus unserer „europazentrischen“ „zentraleuropäischen“ Sicht ... also äh da unten ... also, klar ... fast Afrika. Eben. Irgendwie so. Wird schon stimmmen.)
Also hier nun der Mallingsche Peters:"
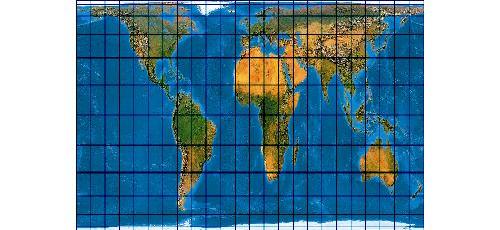
24.12.2010: Natürlich kauft sich ein Kartograph niemals eine Karte mit einer Peters-Projektion. Aber wie bekommt man dann die Projektion in seine Kartensammlung? - Nun ich habe sie einfach auf meinen Weihnachtswunschzettel geschrieben ...
... uns schon hat sie mir der Weihnachtsmann (in Form meiner Tochter Freia) gebracht. Also ... als Weihnachtsgeschenk der eigenen Tochter ... da sieht man es doch gleich mit ganz anderen Augen. Vielleicht ist das Netz doch nicht ganz so completely unsuitable ...
Assemblerprogramme (Direkttransformationen)
Limiting Case of Craster
Gall's Orthographic
Trystan Edwards
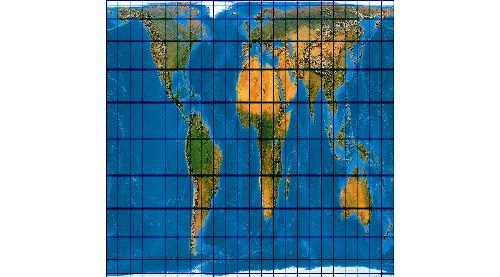
M. Balthasart's Projection 1 (nach Snyder)
M. Baltharsart's Projetion 2 (nach Maling)
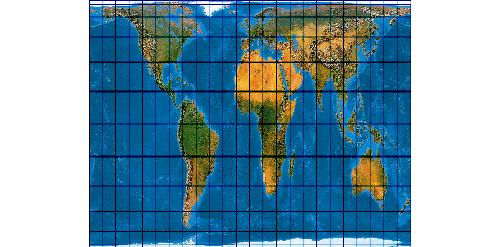
Perters-Projetion 1 (nach Voxland)
Perters-Projetion 2 (nach Maling)
UTM
Ja, aber einmal gibt es Gauß-Krüger, einmal UTM. Hier einmal ganz klar die Aussage: UTM ist Gauß-Krüger. Womit wir wieder beim Thema sind, Kartographie oder Geodäsie. Zugegeben, UTM ist die moderne amerikanische Variante, und die Amis haben da noch so einen Reduktionsfaktor von 99,96 % hineingerechnet. Schnittzylinderprojektion würde man als Kartograph zu Soetwas sagen.
Kann man so machen. Alles einfach ein bißchen verkleinern. Es hat aber doch etwas Pikantes. Diese Vermesser.
Da messen sie nun jahrhundertelang an unsere Erddimensionen herum, und das Ergebnis kann sich auch durchaus sehen lassen. 6378,2 km war der Aquatorradius des alten Helmert und die moderne Satellitengeodäsie hat da noch einmal 45 Meter draufgeschlagen: 6378,245 km. Was für eine Leistung, unsere Mutter Erde so genau auszumessen.
Aber nun kommt da so ein Militär mit dem UTM-System daher und sagt, alles auf 99,96 Prozent verkleinern. Könnte man meinen, so ein paar Zehntel. Aber auf den Erdradius bezogen macht das immerhin etwa 2 1/2 Kilometer aus.
Nun ist die Ellipsenform aber auch nicht allzu ausgeprägt, Polhalbmesser 6356 minus Äquatorhalbmesser 6378, das sind auch gerade einmal 22 Kilometer. Maximalfehler also 11 Kilometer, durchschnittlich weicht die Erdkugel gerade einmal ameist sind es zum , die ganze Exzentrizität , ALso Es kommt aber noch dicker. 150 Jahre Debatte um das richtige Ellipsoid, und dann nimmt man auf einmal ein MaßWas ändere ich messe ich streite ich mich um 45 Meter, wenn dann auf einmal 2 Kilometer schnuppe sind? Es kommt aber noch dicker. Der ganze Unterschied zwischen großer Halbachse (6378 km) und kleiner Halbachse (6356 km) – das sind ja auch nur 22 Kilometer. Da ermittelt man nun jahrhundertelang, Hut ab! Delambre!, kommt auf 22 km Unterschied, wegen denen man eine gigantische Kugelfunktionsrechnerei erfindet. reihenentwicklungen bis zum Getno. Allein die vielen jahrhundertelang gequälten Geodäsiestudenten!
Leute nehmt die Kugel. Die Erde ist rund. Radius 6371 Kilometer. Das ist de Wert von meinem Lehrmeister Prendel. Da gibt es immer irgendwelche Verzerrungern. Gegen die kann man sowieso nichts machen. Das hat übrigens der alte Gauß herausgefunden, als er die Differentialgeometrie erfunden hat.
Hier nun der Witz von Tucholsky mit dem 6396-Eck.
Es gibt da übrigens noch einen Ansatz. Erdumfang 6371 Kilometer und 4,20 Meter. Hä, wieso das? Ganz einfach: 6371004,20 mal 2 Pi ist genau 4020200,00 Meter. Glatt. Da haben wir endlich einmal einen ordentlichen Erdumfang. Und ein Pi, das aufgeht.