[Abbildung: Wagner S. 33]

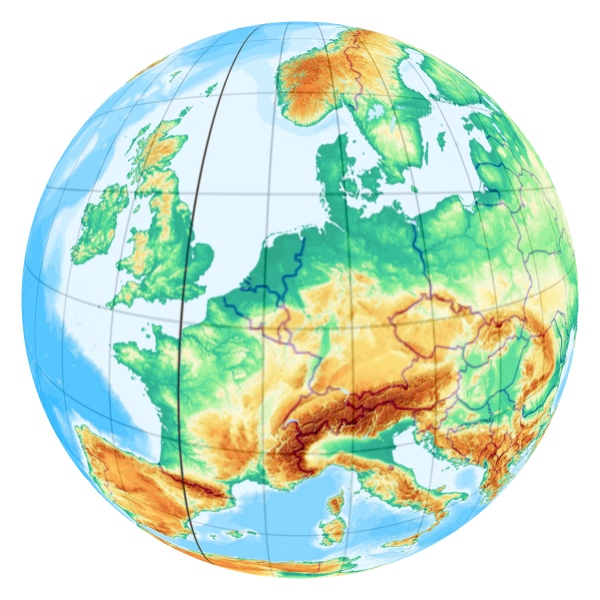
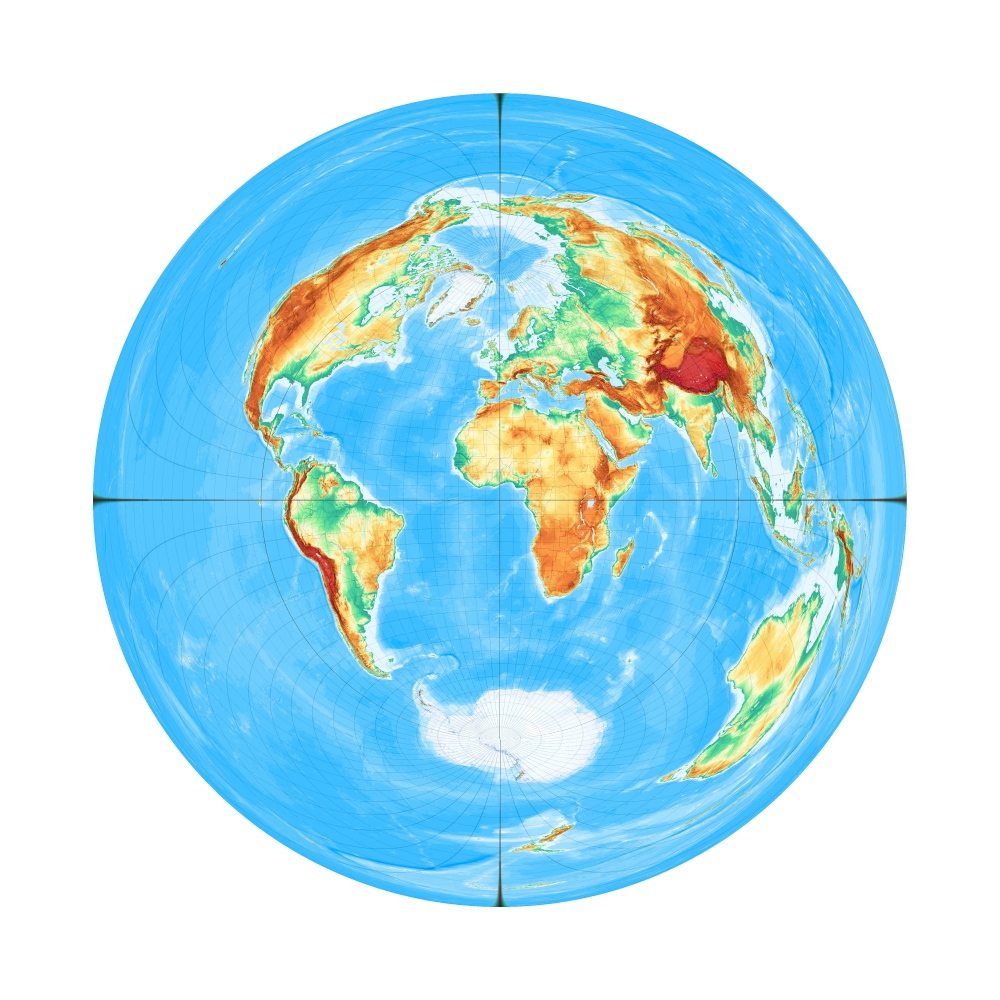
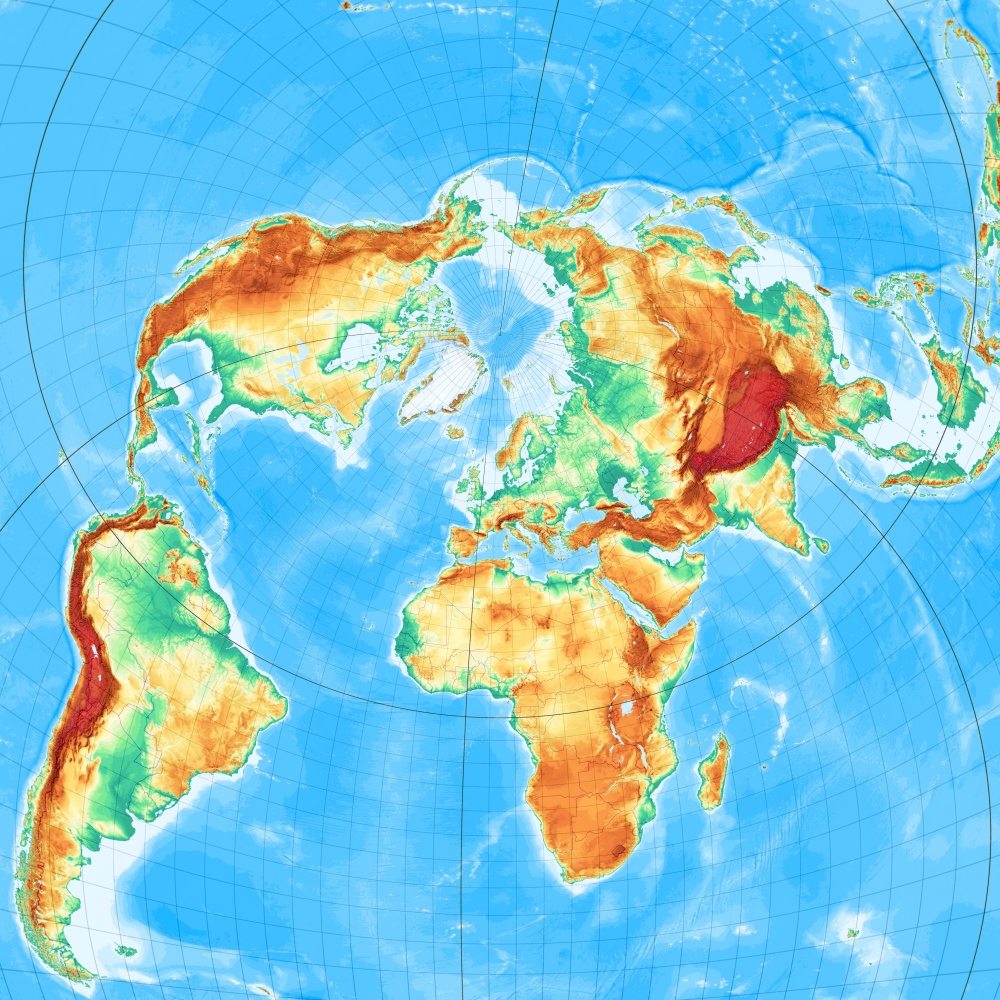
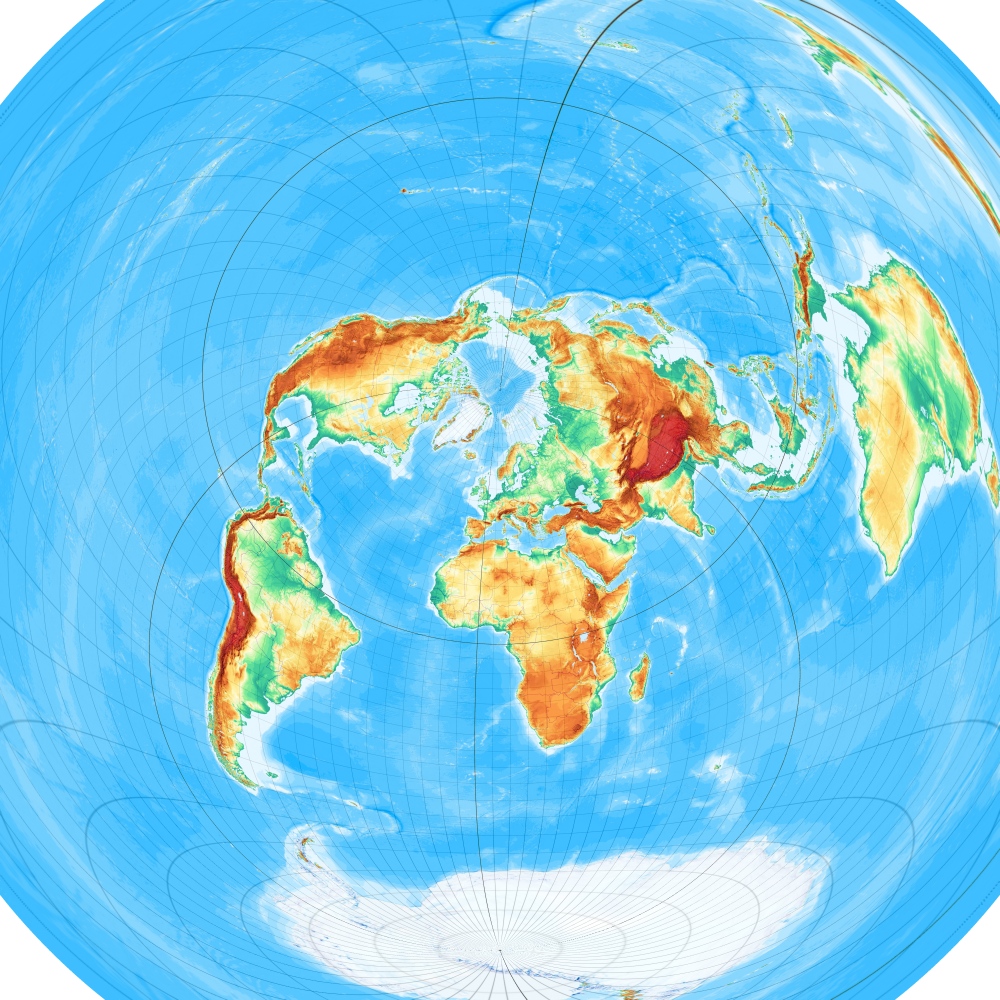
Der allgemeine Fall einer Zentralprojektion von einem Punkt über der Erde. Die typische Projektionsaufgabe, die die Flugsimulation stellt.

Die Erde, wie sie aus einer Höhe von 400 km über 51°N, 7°O aussieht:

(Maßstab 1:10.000.000)

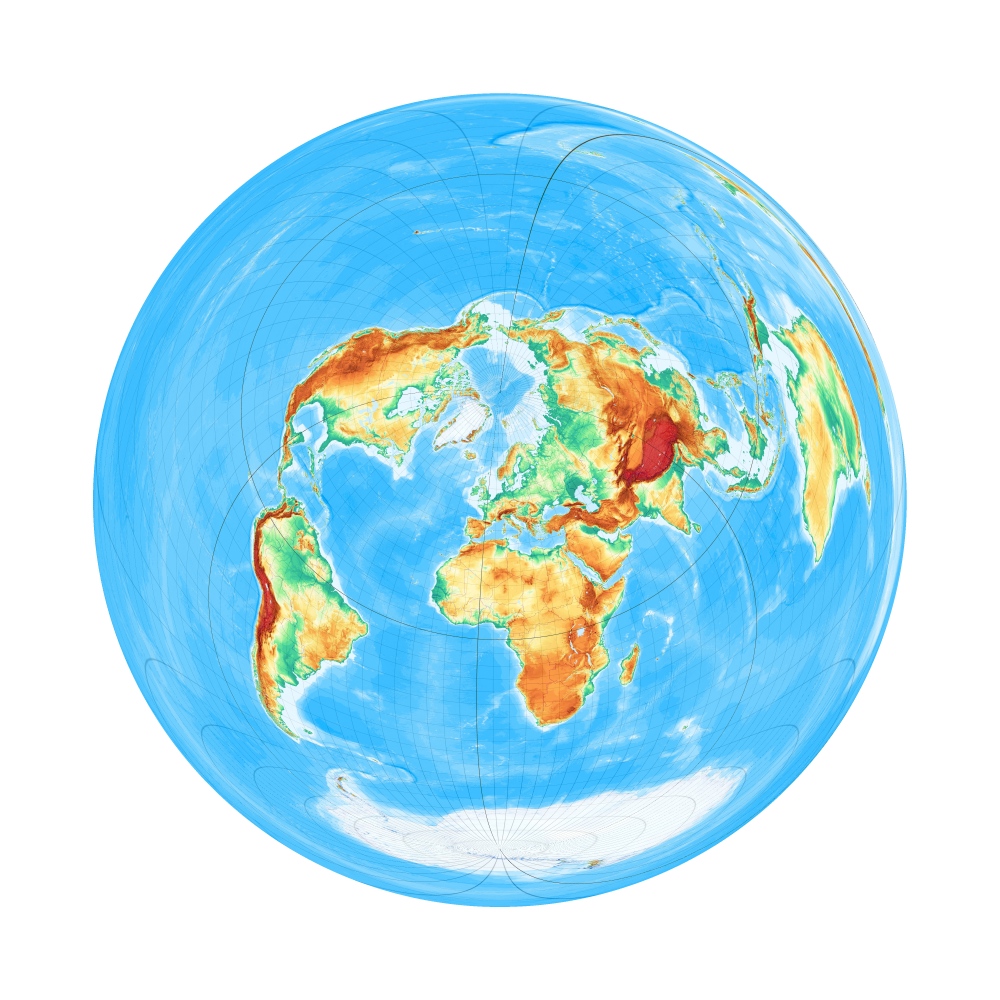
Der Breusing ist der bekannteste 2b-Azimutalentwurf. Er ist das geometrische Mittel aus winkel- und flächentreuem Azimutalentwurf und wird, weil er formal etwa gleichwertig dem abstandstreuen Azimutalentwurf ist, mitunter als etwas überflüssig angesehen und belächelt.

Breusing, polständig:

So schlimm ist Breusings Entwurf aber nun gar nicht. Insbesondere hat er in querachsigen und schrägen Lagen, wo der abstandstreue Azimutalentwurf schnell zum "Quetschen" neigt, ausgewogenere Gitternetzformen, wohl von seinem stereographischen "Elternteil" geerbt.

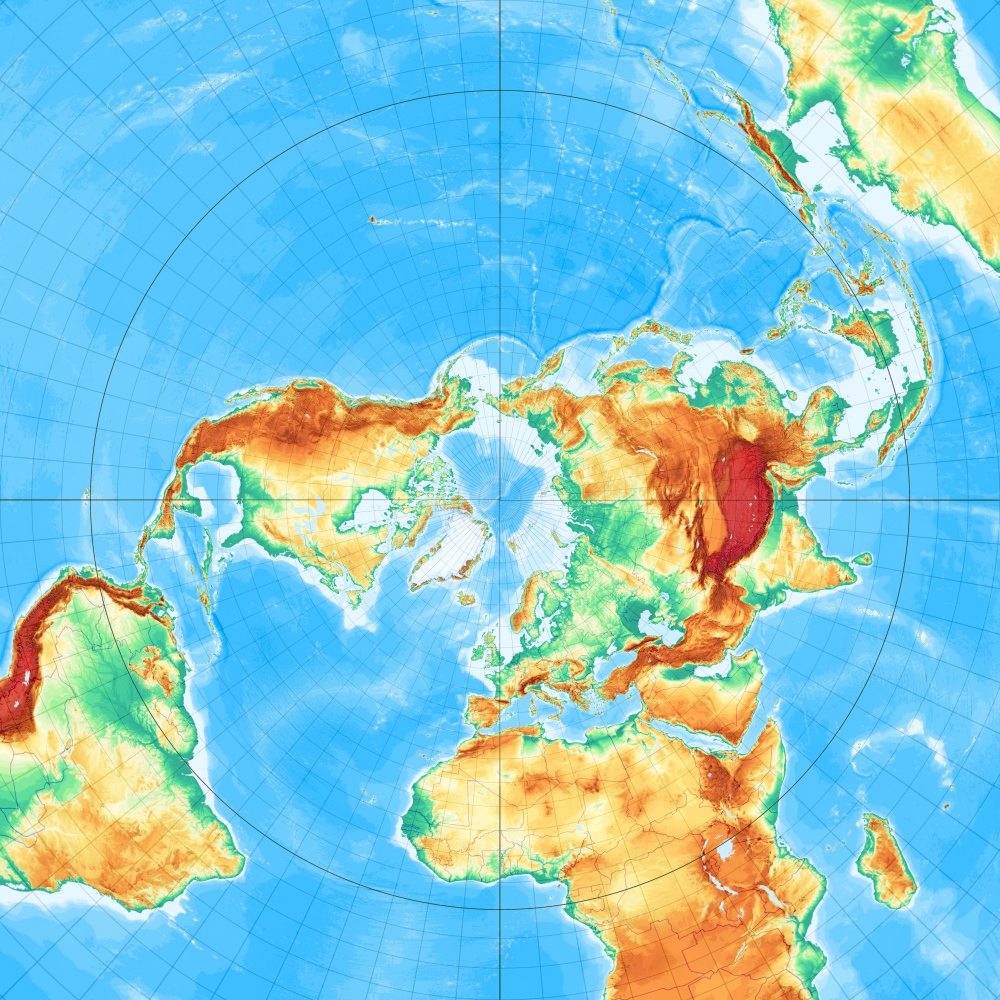
Breusing, querachsig:

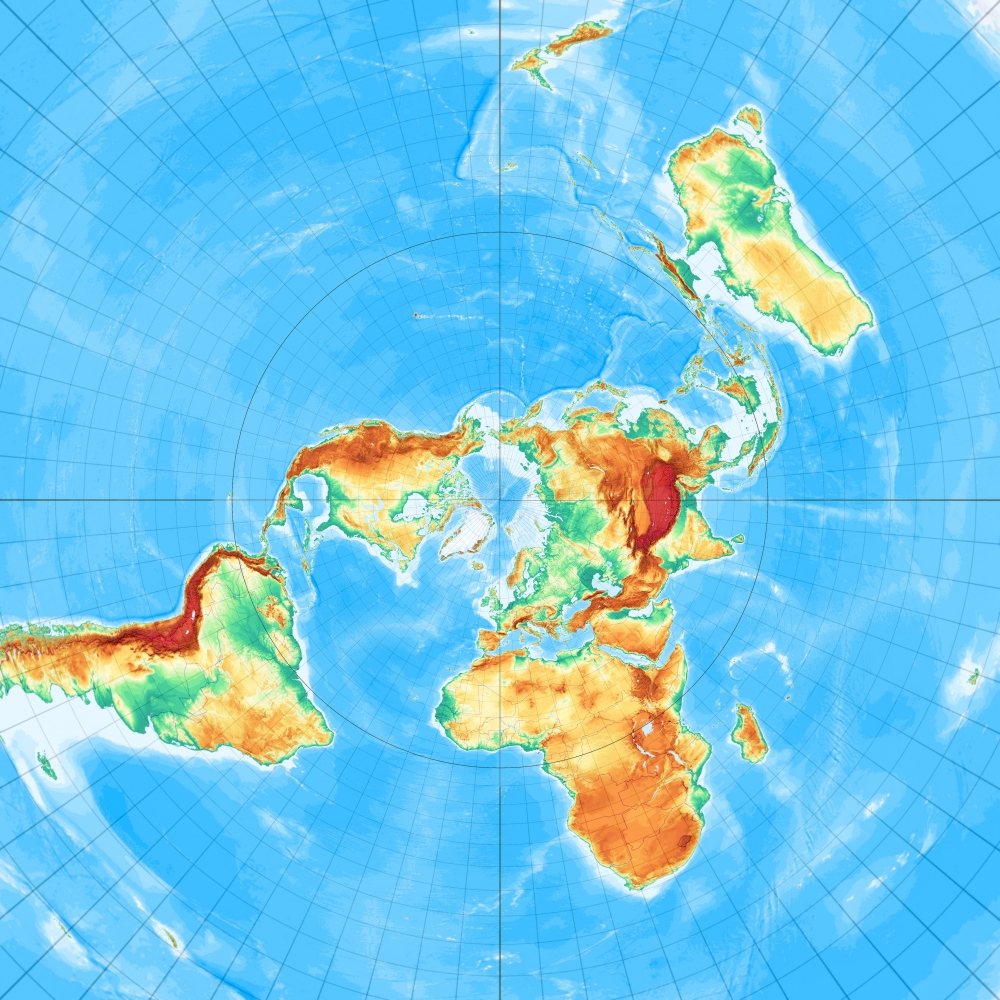
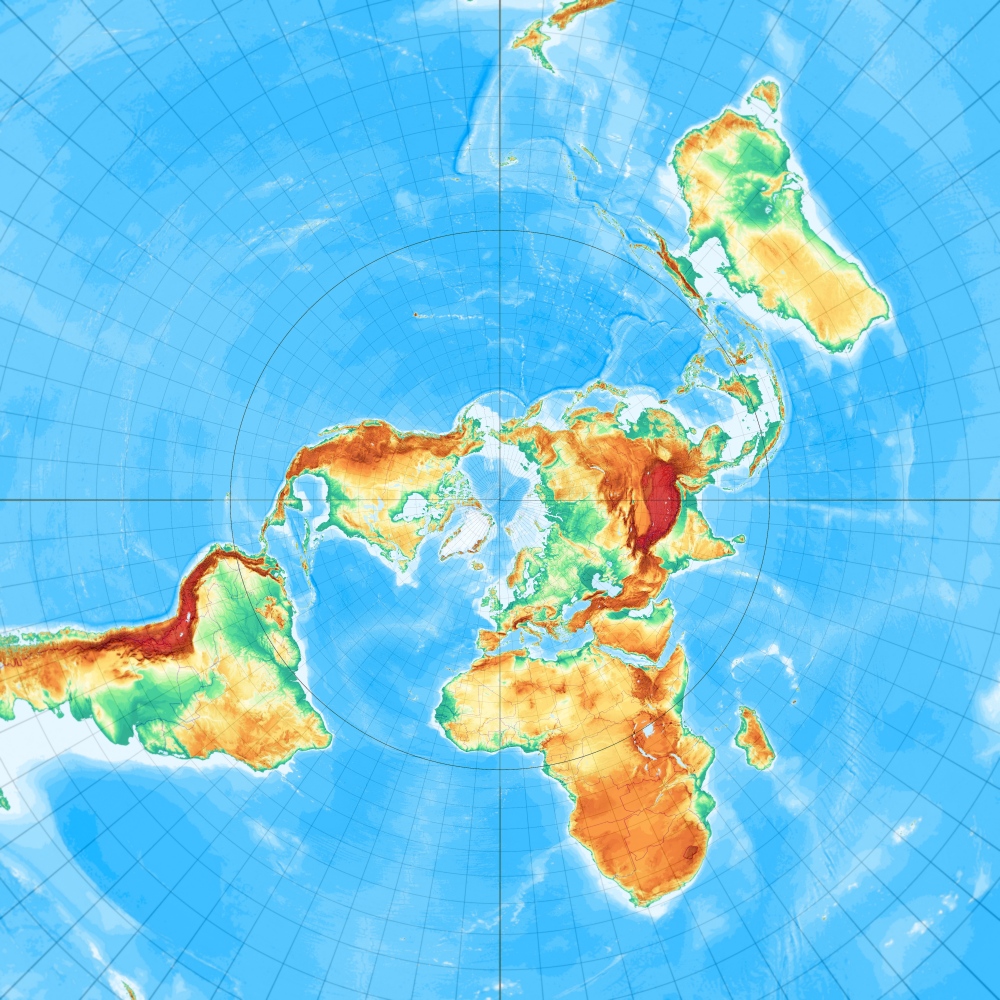
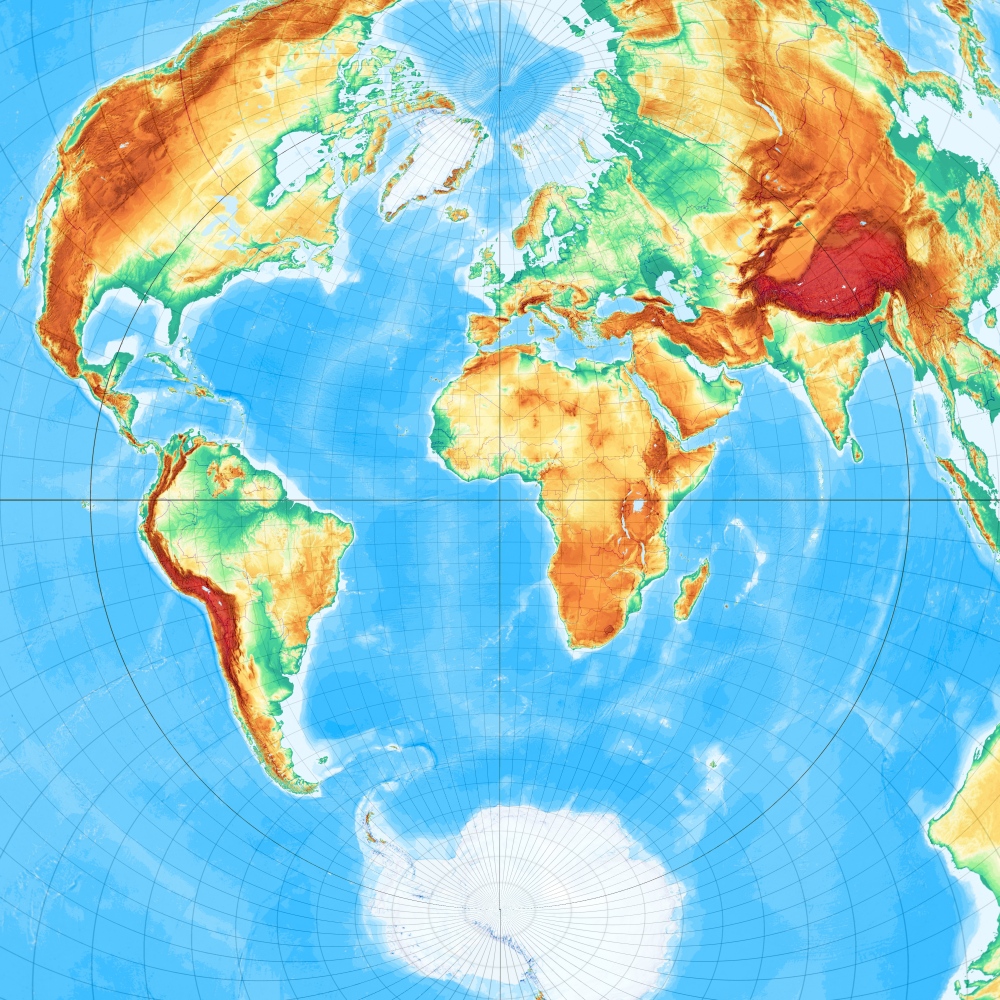
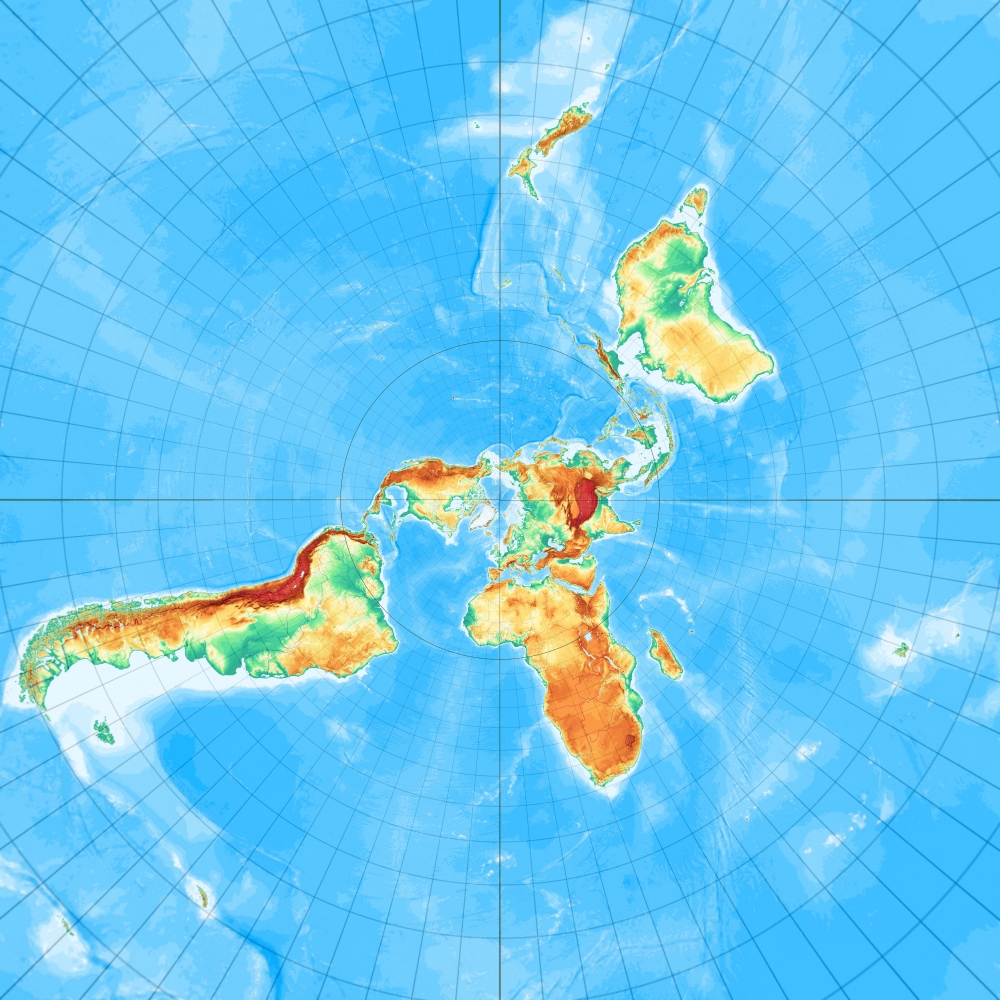
Und das ist "der Breusing" in Schräglage mit Berührungspunkt 51° Nord und 7° Ost (wie alle auf dieser Seite vorgestellten azimutalen Schräglagen; eine Referenz an Tobias Jungs Map-Projection-Seite.

Airys Minimum-Error Azimutalprojektion

Polständig oder erdachsig (Wagner empfiehlt, diese Lage besser nicht als "normal" zu bezeichnen, denn in der Mathematik steht die Normale auf der Tangente senkrecht.)

Airy Minimum Error Azimuthal, transversal oder querachsig

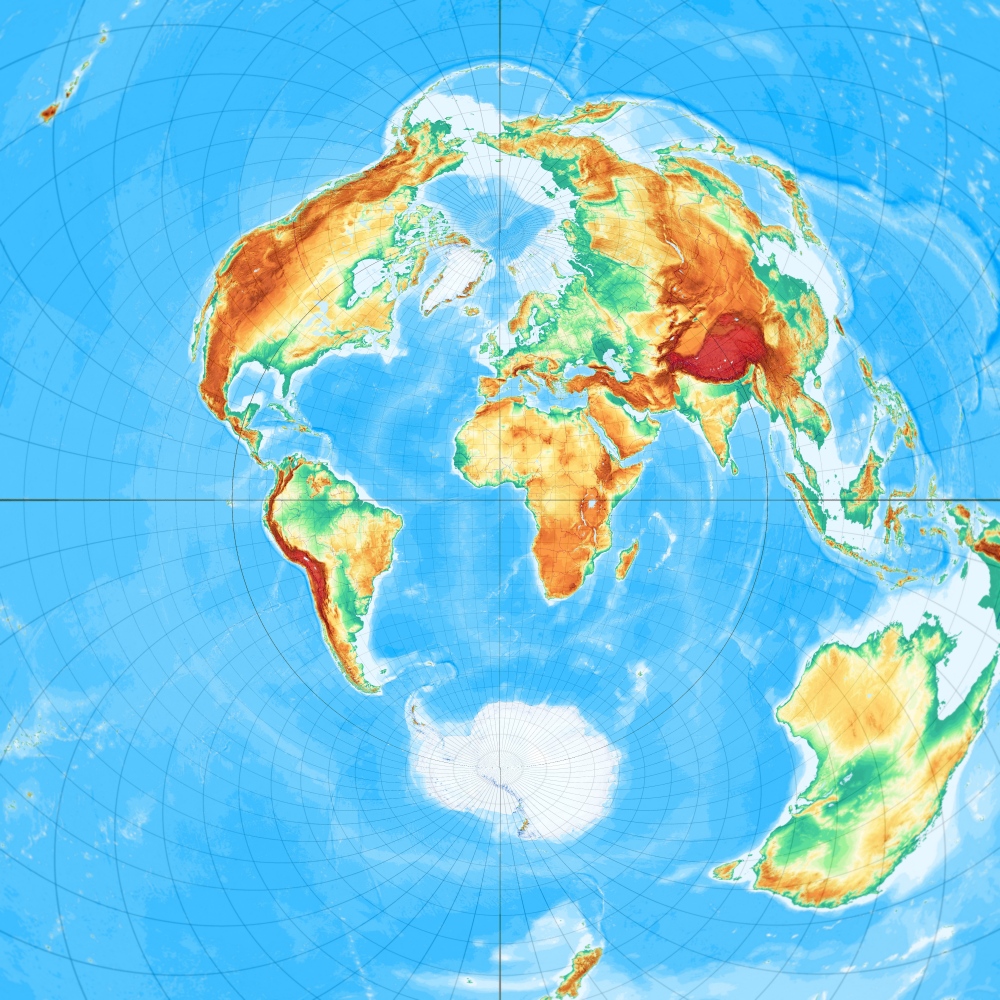
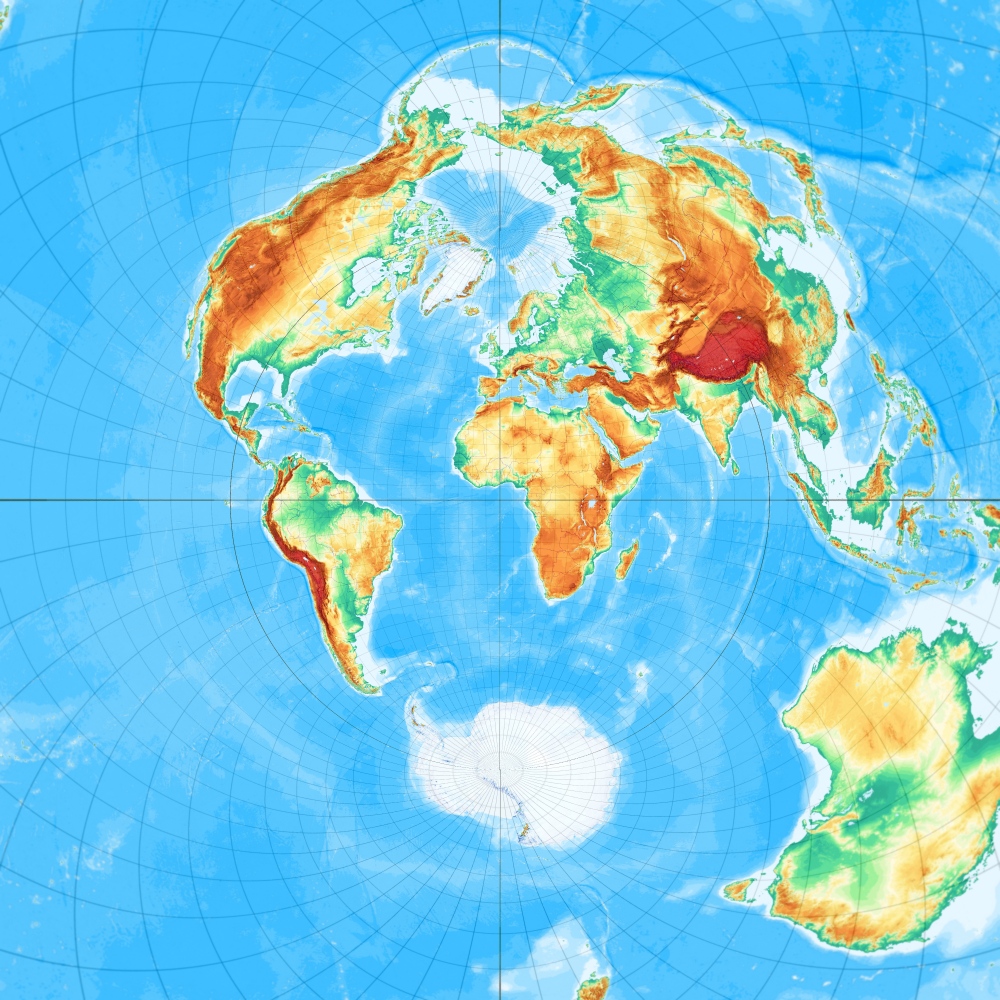
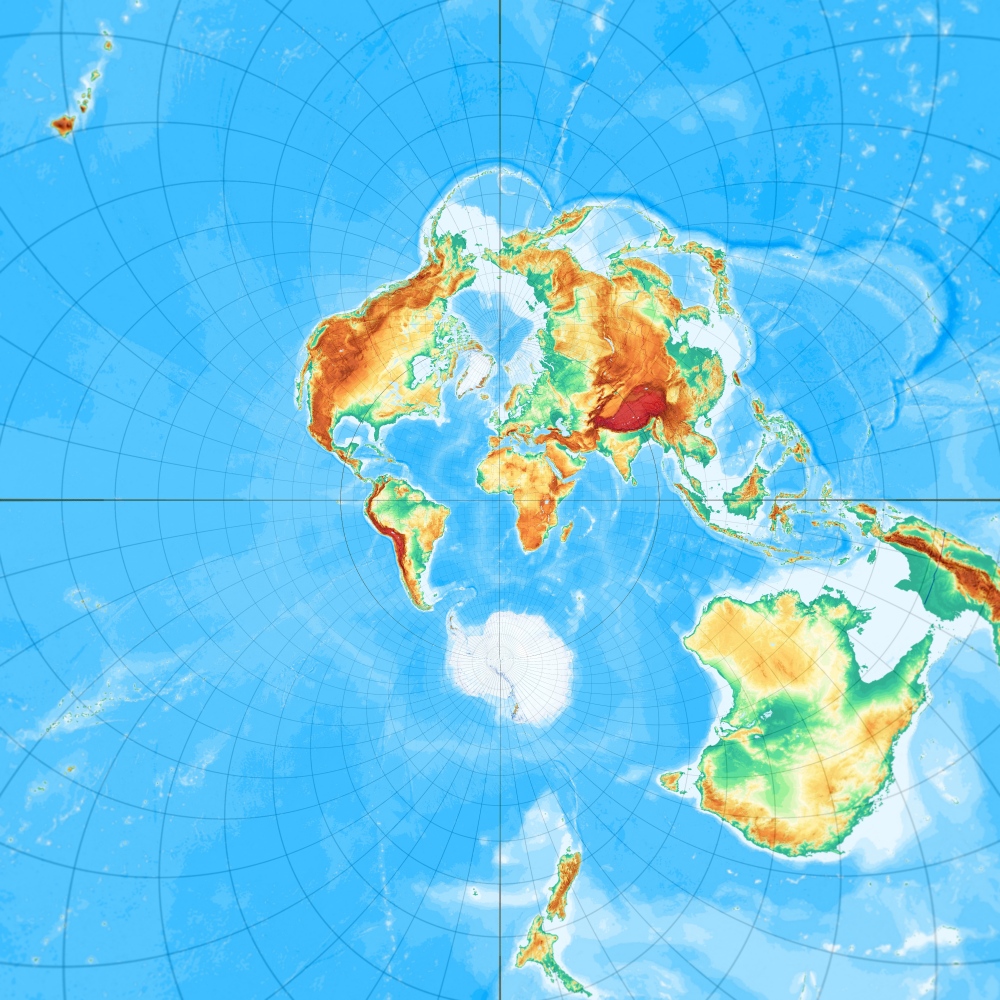
Airy Minimum Error Azimuthal, frei oder schiefachsig

Ginzburgs Azimutalprojektion ...

... ist eine Verallgemeinerung der azimutalen Sinusentwürfe. Die Formel enthält einen Parameter k, und erzeugt bei k=1 einen orthographischen und bei k=2 einen flächentreuen Azimutalentwurf. Hier einmal ein k=3-Ginzburg. Grob ergibt ein derartiges "Über-flächentreu" ein vermittelndes, grob etwa abstandstreues Netz.

Anmerkung: Ich reserviere mir hier schonmal die Primogenitur des entsprechenden Tangens-Analogons, also eines Netzes, das bei k=1 die gnomonische und bei k=2 die stereographische Azimutalprojektion ergibt. Das wird dann bei k=3 ebenfalls recht hübsch vermittelnd werden ...

Polständig oder erdachsig

Ginzburg azimutal (mit k=3), transversal oder querachsig

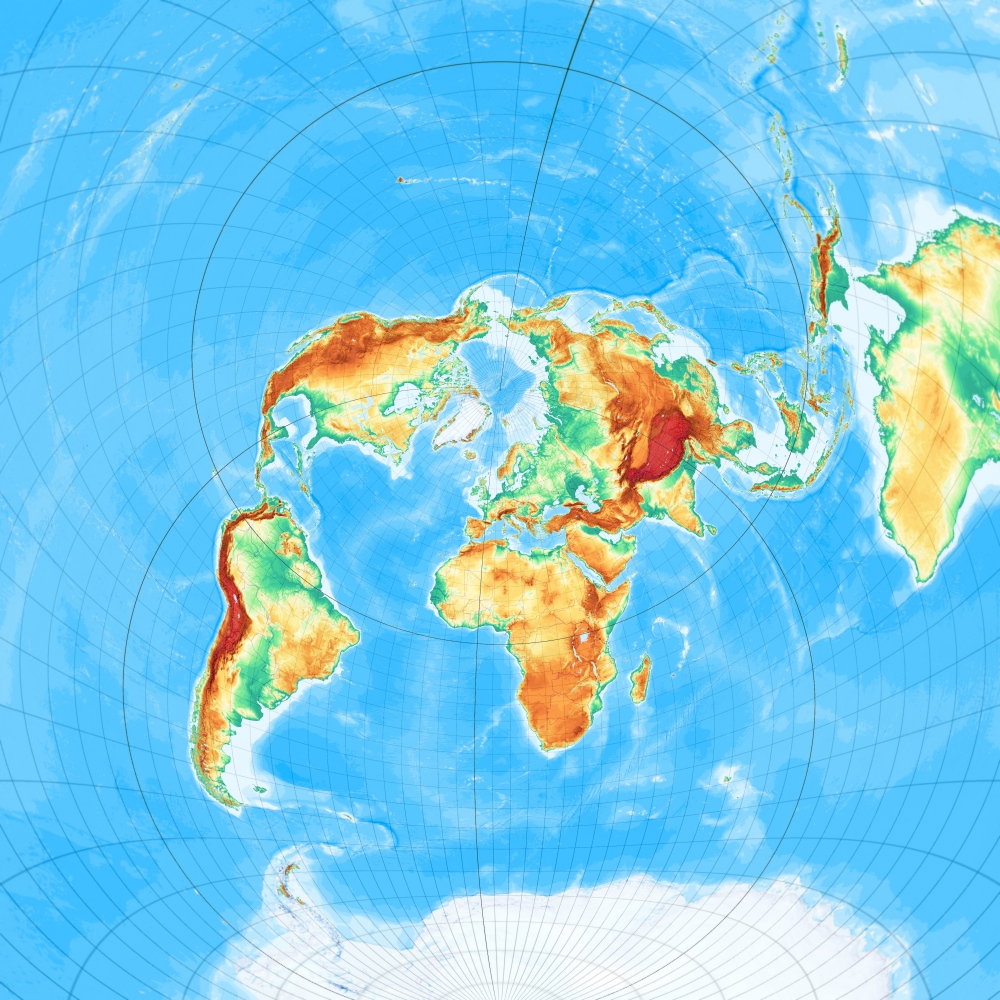
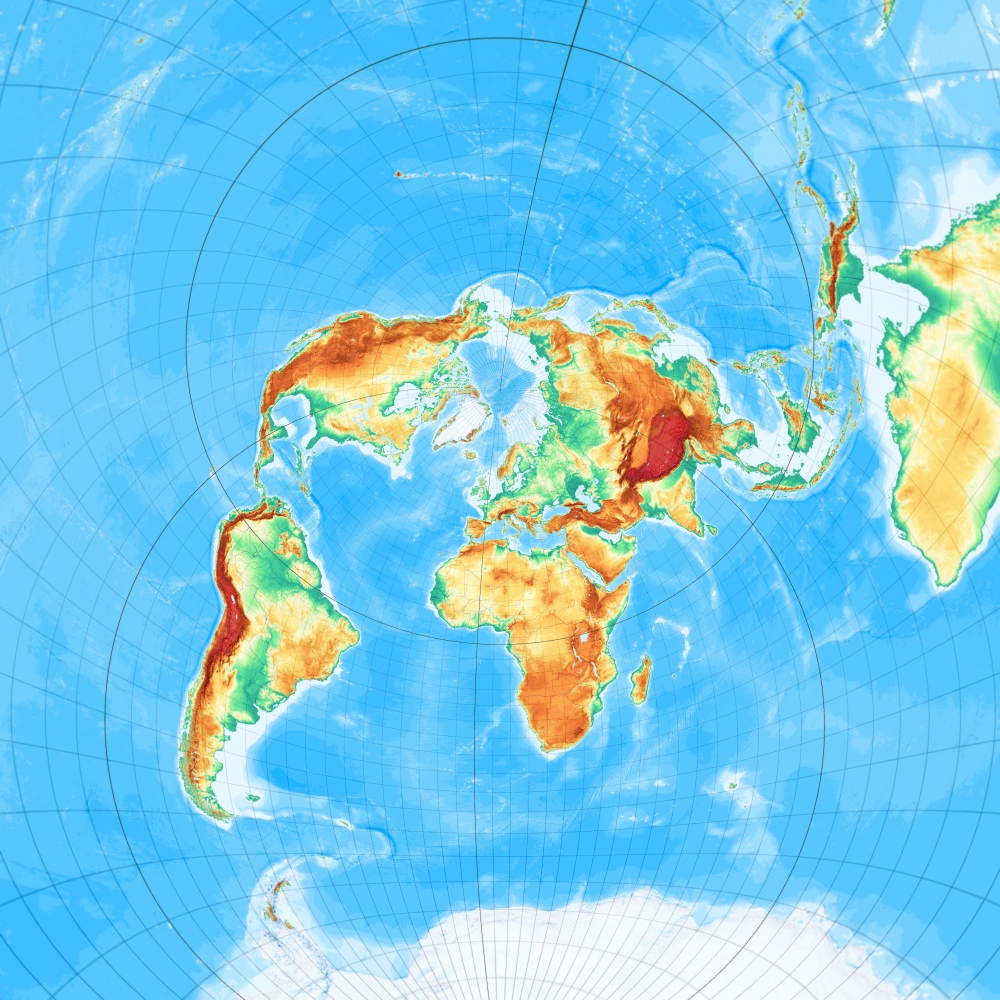
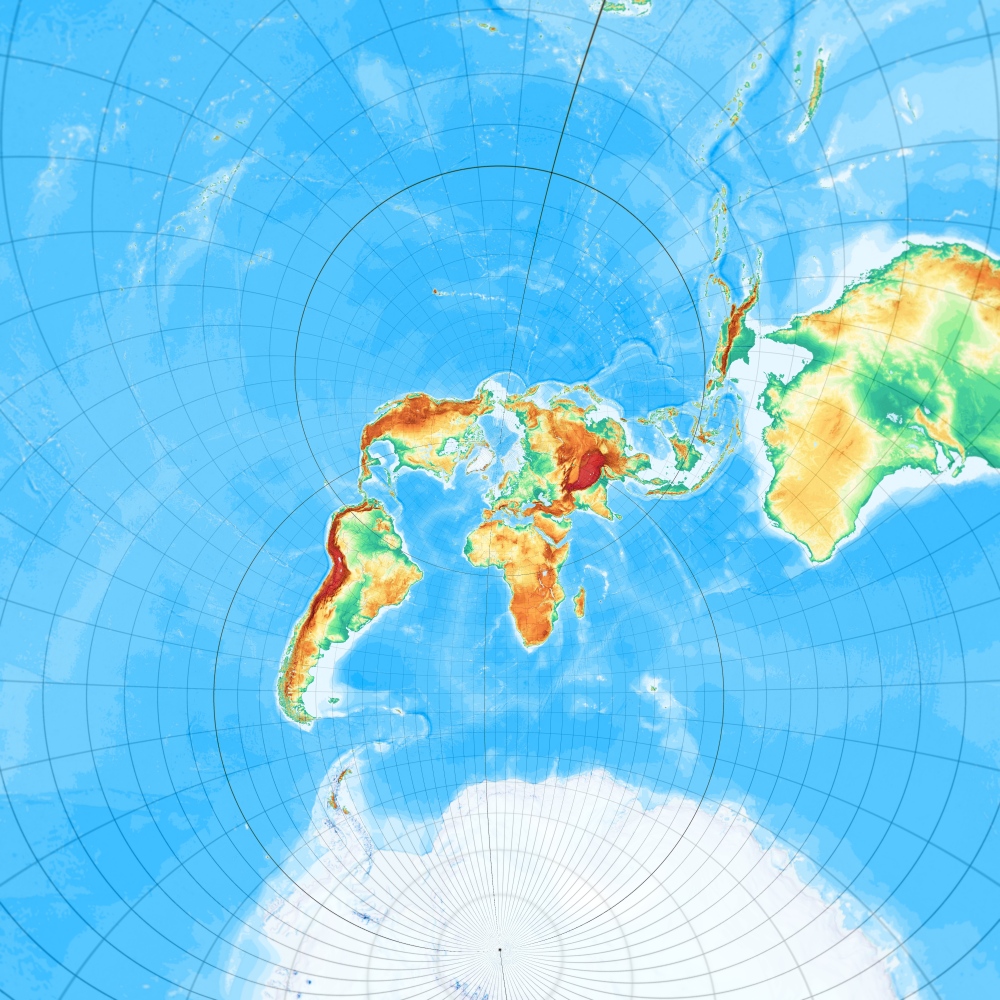
Ginzburg azimutal (mit k=3), frei oder schiefachsig

Nells Azimutalprojektion

Nach Britta Bernecker: Adam Maximilian Nell 1852

Polständig oder erdachsig

Nell, transversal oder querachsig

Nell, frei oder schiefachsig

Die Lagrangesche Projektion ...

... ist eine Projektion vom Gegenpol des Kartenmittelpunktes auf eine Ebene durch den Erdmittelpunkt. Das ist nun nicht ganz neu, sondern eine stereographische Azimutalprojektion auf 50 % verkleinert.

(Lagrange steckt hier übrigens nicht nur im Netz, sondern auch extra nochmal in jedem Pixel. Die wurden nämlich mit Lagrangeschen Interpolationspolynomen interpoliert. Wenn dass der olle Lagraange wissen würde ...)

Lagrangesche Projektion, polständig

Lagrangesche Projektion, transversal oder querachsig

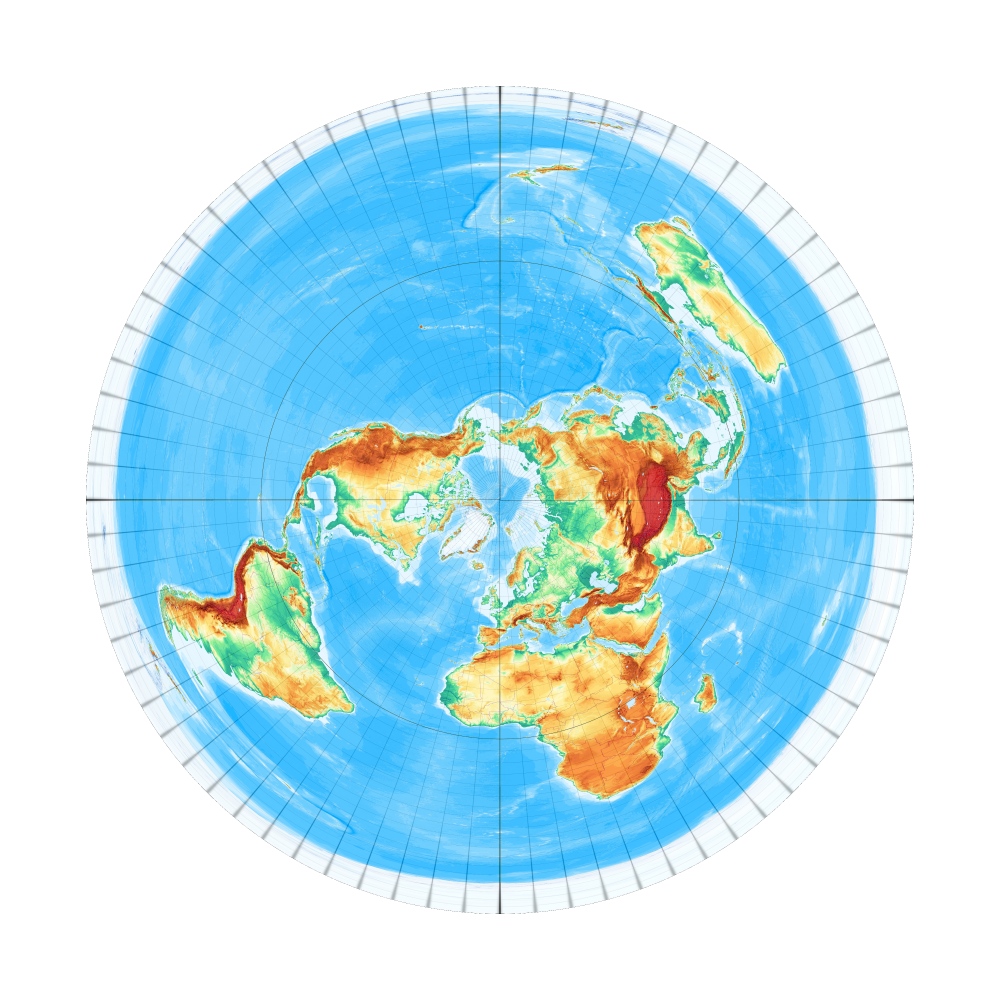
Lagrangesche Projektion, frei oder schiefachsig

Solovyevs Azimutalprojektion

Der Solovyev wurde mir freundlicherweise von Prof. Tobler mitgeteilt: Tobler, W.: Some Notes on azimuthal projections. Student paper. Nov. 1979. - Zit. nach A. V. Graur, Matematiceskaya Kartografia, Leningrad 1956. Best regards to Prof. Waldo Tobler, Santa Barbara.

Polständig oder erdachsig

Solovyev, transversal oder querachsig

Solovyev, frei oder schiefachsig

Assemblerprogramme

Weil Karten nur ganz selten Nord- oder den Südpol abbilden sollen, sind die in der akademischen Theorie polständig zitierten Formeln zahnlose Tiger. Aus diesem Grund wurde in allen Programmen eine Transformation in eine freie Lage mit eingebaut. Dies kostet zwar Code und Rechenzeit, gibt den "Akademikern" aber überhaupt erst den nötigen Biss, mit dem sie in der freien Wildbahn der Praxis überhaupt erst einsetzbar werden.

Allgemeine perspektive Abbildung einer Kugel auf eine Ebene (Direkttransformationen)
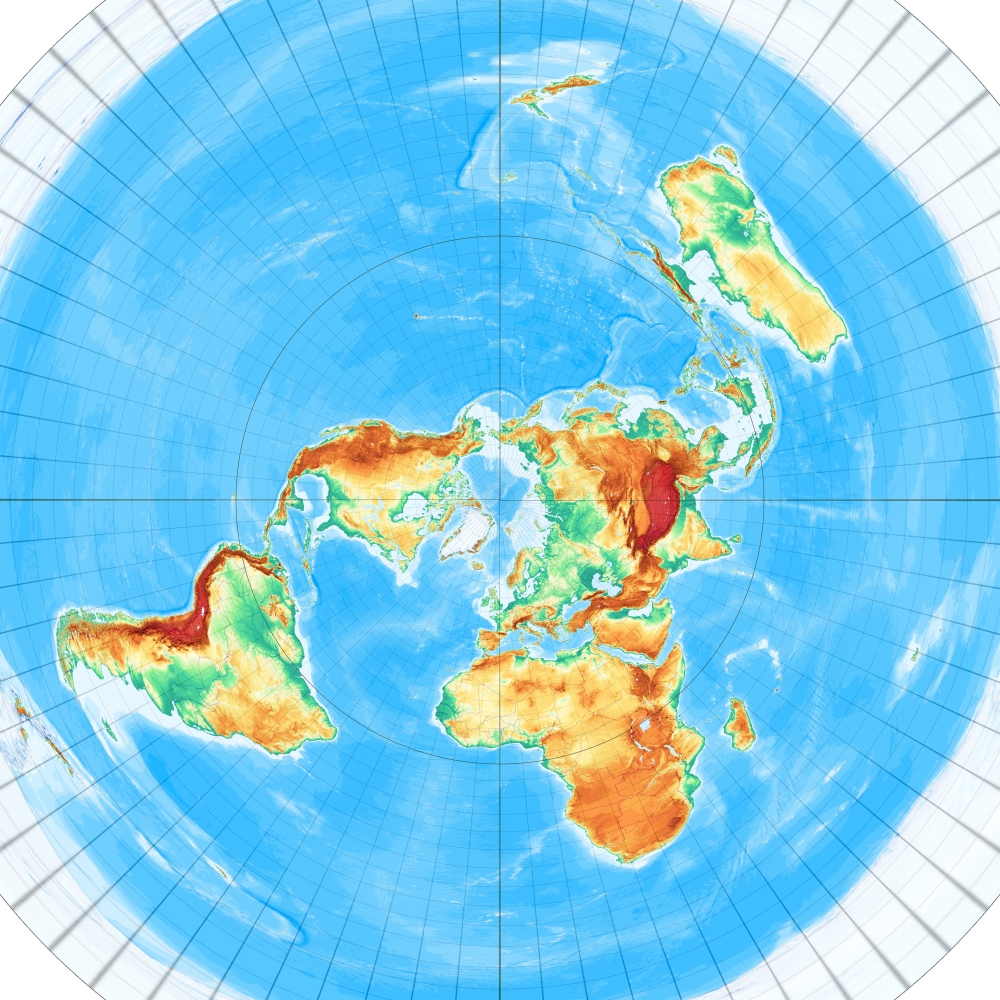
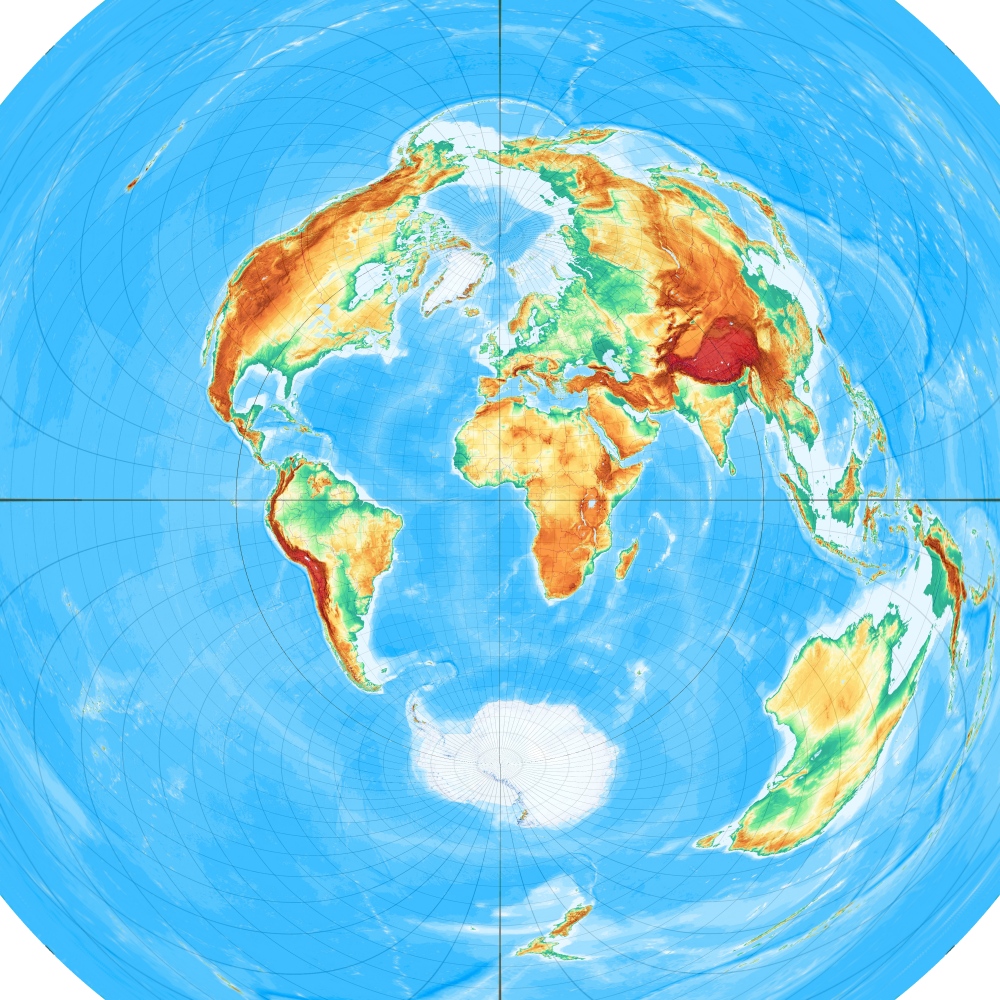
Breusings vermittelnder Azimutalentwurf, freie Lage (Direkttransformationen)
Airys Minimum-Error Azimutalprojektion, freie Lage (Direkttransformationen)
Ginzburgs Azimutalprojektion, freie Lage (Direkttransformationen)
Nells Azimutalprojektion, freie Lage (Direkttransformationen)
Lagrangesche Projektion, freie Lage (Direkttransformationen)
Solovyevs Projektion, freie Lage (Direkttransformationen)

17.03.2021: Kartenreihe World 1:100.000.000 (W100)

17.03.2021: Kartenreihe World 1:100.000.000 (W100)