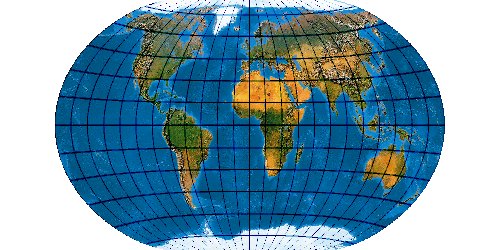
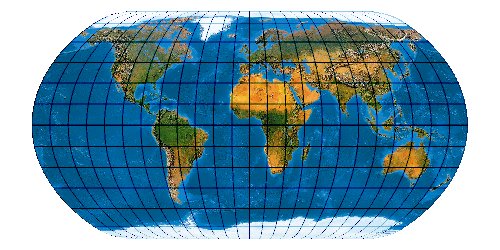
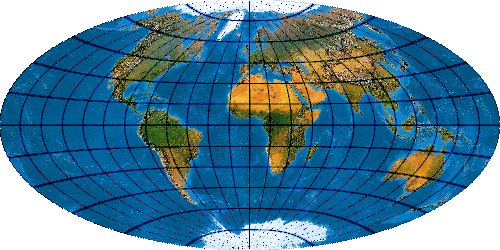
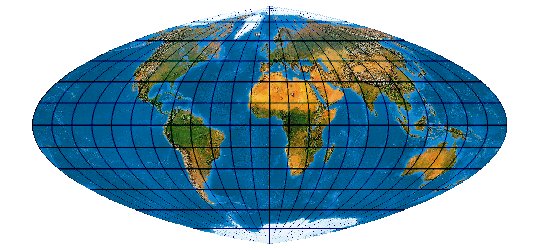
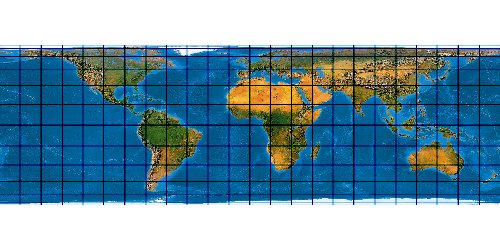
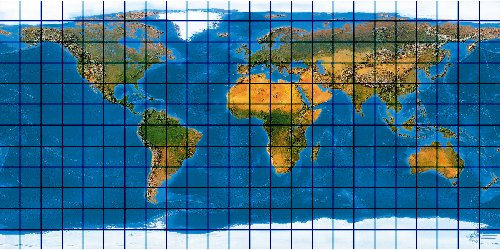
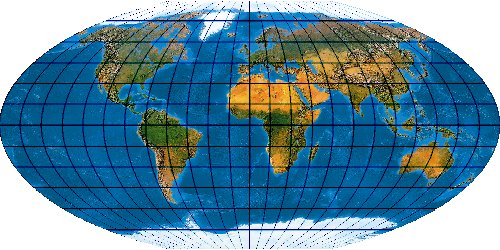
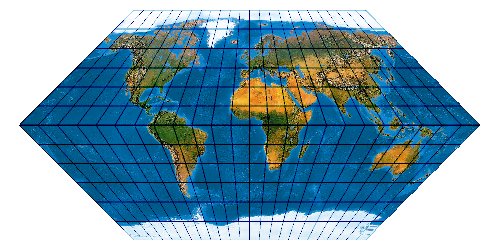
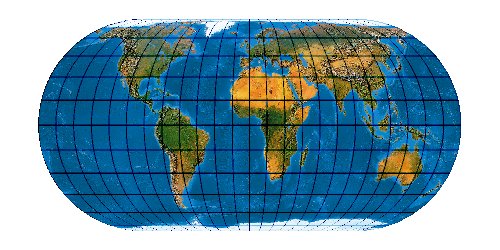
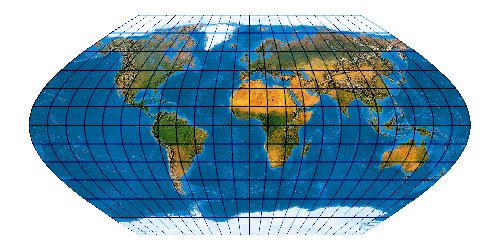
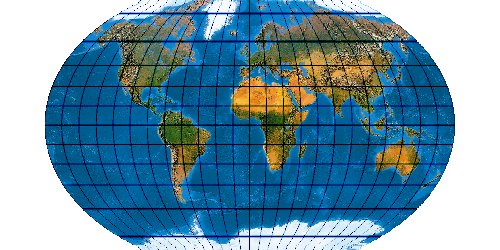
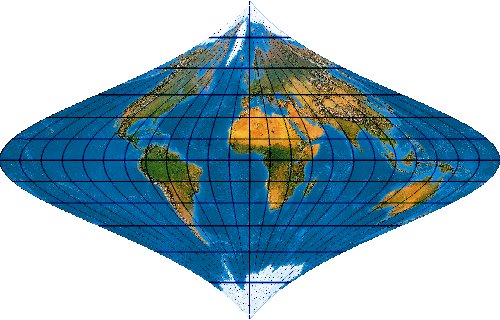
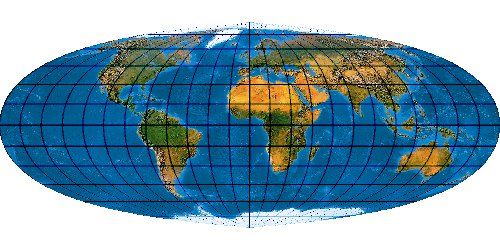
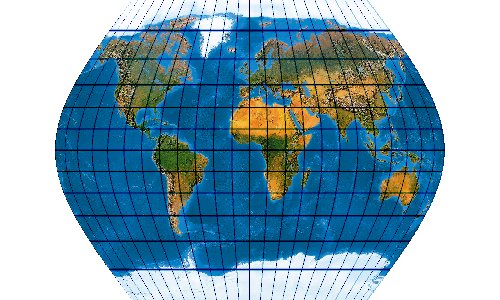
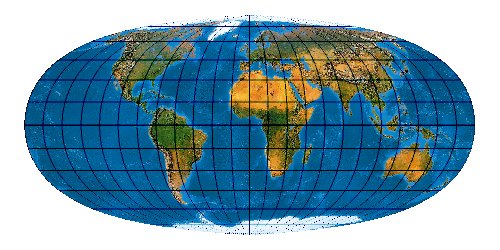
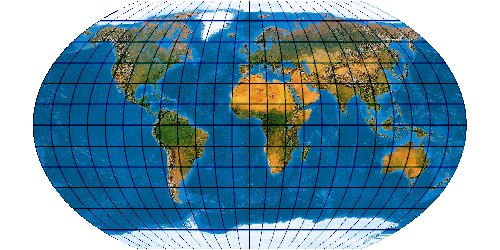
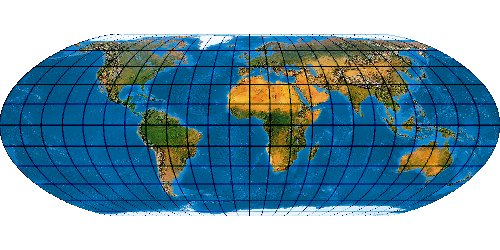
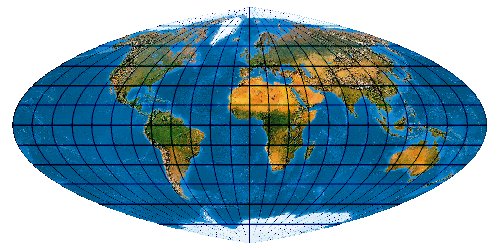
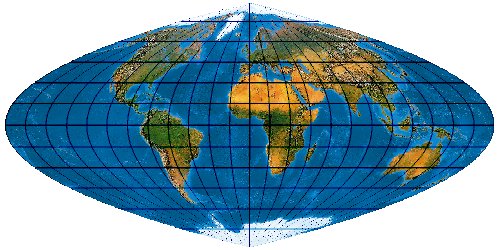
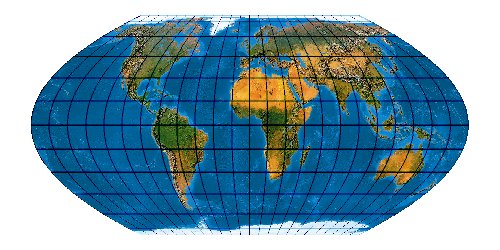
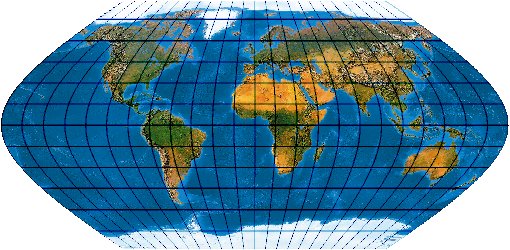
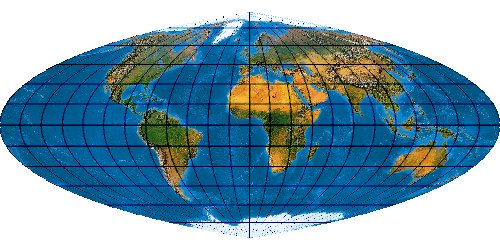
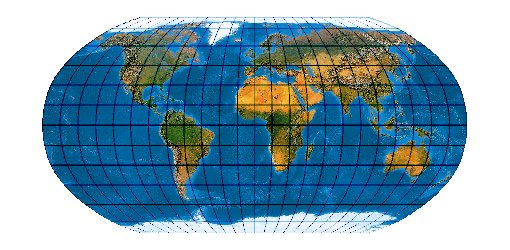
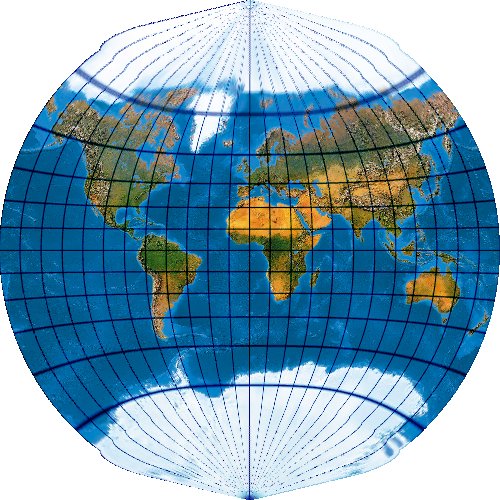
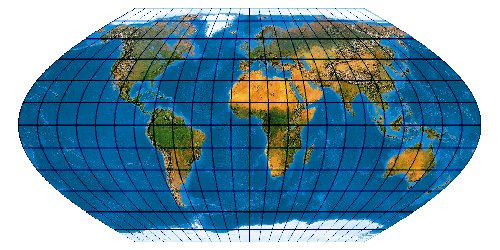
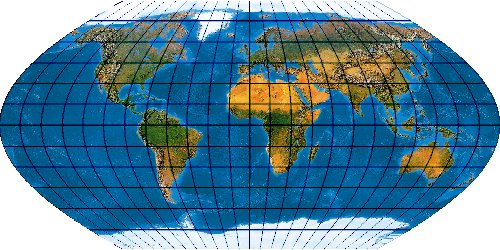
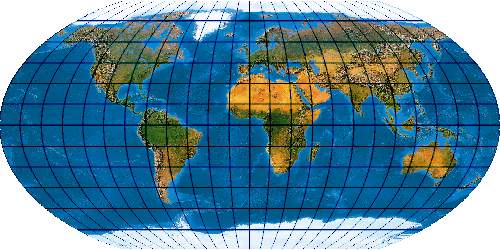
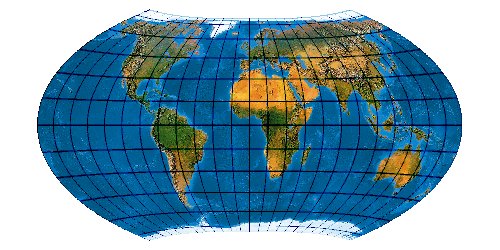
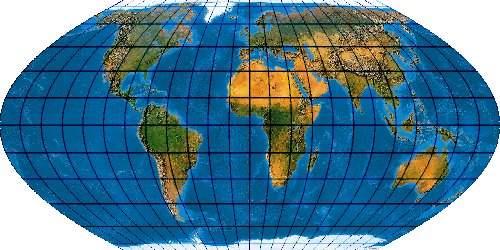
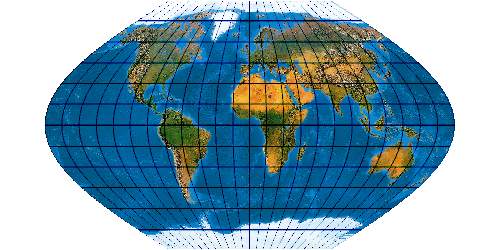
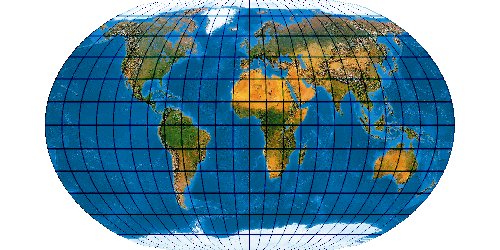
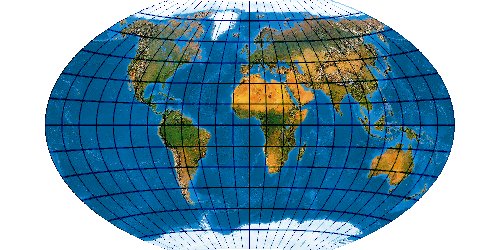
|
Mit der wachsenden Anzahl bekannter Kartennetze wird es immer schwieriger, deren Komplexität einigermaßen zu beherrschen. Es stellt sich die Frage nach einem allgemeinen Verfahren, mit dem eine möglichst große Anzahl von Kartennetzen hergestellt werden kann. Bernhard Jennys Flex Projector ist eine interessante Antwort auf diese Frage.
Was verbirgt sich hinter dem Flex Projector? — Kartenprojektionen werden gewöhnlich mit einer Formel berechnet. Das trifft im Prinzip auch für die ab 1961 von Arthur H. Robinson entwickelte Robinson-Projektion zu – aber eben nur im Prinzip. Robinson rechnet nicht mit einem expliziten Formel, die z. B. Winkelfunktionen nutzt – sondern mit tabellierten Zahlenwerten. Je eine RX- und eine RY-Koeffiziententabelle verzeichnet Stützstellen im Abstand von 5°. Über diese Stützstellen werden Funktionen interpoliert. Mit diesen wird letztendlich eine Abbildungsfunktion modelliert.
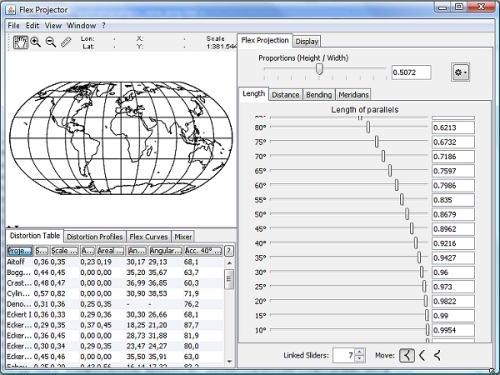
Der Schweizer Kartograph Bernhard Jenny (ETH Zürich) hat – angeregt durch den Amerikaner Tom Patterson (U. S. National Park Service) – dieses Prinzip weiterentwickelt. Sein auf der Seite www.flexprojector.com vorgestelltes Verfahren gestattet nun nicht nur das Rechnen mit den festen „Robinson-Koeffizienten“, sondern mit weitgehend beliebigen Werten. Auch hat er den beiden Robinsonschen Reihen RX („Length“) und RY („Distance“) zwei weitere Reihen RB („Bending“) und RM („Meridian Distribution“), sowie einige weitere Variablen hinzugefügt.
So lassen sich sehr viele Projektionen herstellen. Es ist verblüffend, wie genau sich bekannte Kartennetzentwürfe mit dem Flex Projector approximiieren lassen. Es muss aber gar nicht unbedingt ein bekanntes Netz sein. Jenny und Patterson nutzen den Flex Projector auch für Neuentwicklungen ...
Neuentwickelte Flexprojektionen
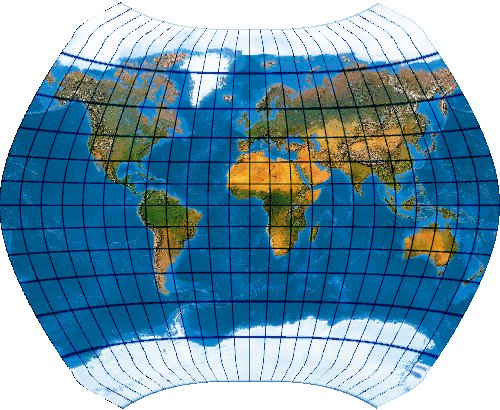
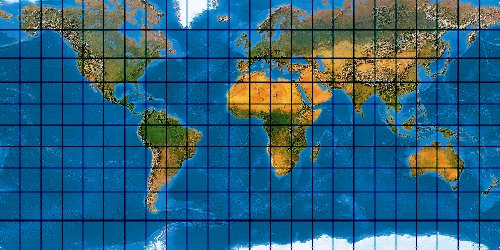
A4 Projection
A4 Projection im Großformat
(1:200.000.000 bei 254 dpi, 700 kByte)
Jennys A4 ist eine Netz-Neuentwicklung, die ihren Namen dem günstig
auf ein Blatt A4 skalierbaren Kartenformat verdankt.
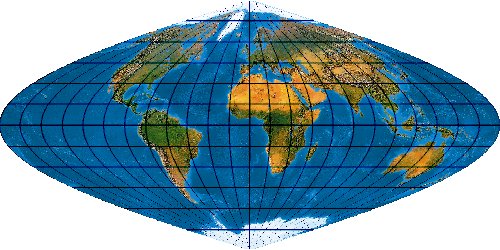
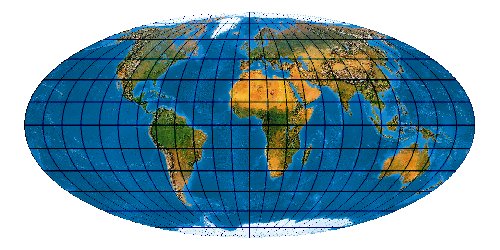
Natural Earth Projection
Flexprojection Natural Earth im Großformat
(1:200.000.000 bei 254 dpi, 700 kByte)
In der Natural Earth hat Tom Patterson eine Reihe wunderbarer
naturnaher Landschaftskarten der Erde berechnet.
Approximationen bekannter Netzentwürfe mit dem Flex Projector
Je nachdem, wie gut das Interpolationsverfahren die originale Formel anzunähern in der Lage ist,
nähern sich die Flexprojektion und Originalabbildung mehr oder weniger gut an.
Aïtoff (Flex Projection)
Boggs Eumorphic (F. P.)
und ergibt darüberhinaus exakt das Andersonsche Längen-Breiten-Verhältnis von 1:2. Fast glaube
ich, dass meine Originalrechnung einen Fehler hat. (Evendens Formel
nutzt Sekansfunktionen, was hinterfragbar ist. Ich habe diese in Cosinüsse umgeformt, tja ... ob da
so im Detail wirklich der originale Boggs rausgekommen ist? Ich schlage nach, finde
aber in dem Handexemplar meines Diophant-
- äh - Evenden-Manuskriptes nur eine sehr dünne Bleistift-Notiz ...)
Cylindrical Equal-area (Flächentreuer Zylinderentwurf) (F. P.)
Cylindrical Equidistant (Abstandstreuer Zylinderentwurf oder quadratische Plattkarte) (F. P.)
Denoyer (Semi Elliptical) (F. P.)
Eckert-Greiffendorf (F. P.)
Eckert I (F. P.)
Eckert III (F. P.)
Eckert IV (F. P.)
Eckert V (F. P.)
Fahey (F. P.)
Foucault (F. P.)
Foucault Sinusoidal mit n = 0,5 (F. P.)
Der Foucaut Sinusoidal enthält einen Parameter n, der den Entwurf zwischen einem flächentreuen
Zylinderentwurf und einem Mercator-Sanson variiert. Jenny rechnet mit einem n-Wert von 0,5.
Gall Stereographic (Galls stereographische Zylinderprojektion) (F. P.)
Ginsburg VIII (F. P.)
Goode Homolosine (F. P.)
Kavraiskiy V (F. P.)
Kavraiskiy VII (F. P.)
Larrivée (F. P.)
McBryde-Thomas Flat-Polar Sine (No. 2, F. P.)
Mercator-Sanson (Sinusoidal) (F. P.)
Miller Cylindrical No. 1 (F. P.)
Mollweide (F. P.)
Nell-Hammer (F. P.)
Putnins P1 (F. P.)
Putnins P4 (F. P.)
Putnins P'4 (F. P.)
Putnins P'5 (F. P.)
(Adams) Quartic Authalic (F. P.)
Robinson-Projektion (F. P.)
Allerdings gibt es bei Breite 40° unerklärlicherweise einen ganz
kleinen Versatz, den ich nicht aufklären konnte. Ich kann nicht ausschließen, dass es an meiner Implementation liegt.
Van der Grinten I (F. P.)
Die Unstetigkeiten in Polnähe fallen, da das Netz oft nur in zentralen Lagen genutzt wird,
praktisch wenig ins Gewicht. Erinnert sei hier auch an die ebenfalls nur zentral
gerechneten Wagnerschen van der Grinten-Adaptionen Wagner Y3 und Wagner Y4.
Wagner II (F. P.)
Wagner III (F. P.)
Wagner VI (F. P.)
Wagner VII (F. P.)
Werenskiold I (F. P.)
Winkel I (F. P.)
Winkel II (F. P.)
Der berühmte Winkel Tripel (F. P.)
Das Bild entspricht dem gelegentlich in der Literatur anzutreffenden „schmalen“ Winkel Tripel. Mein eigener
Winkel Tripel (der auch dem Klett-Perthes-Winkel-Tripel entspricht) läuft etwas breiter.
Alle Netze wurden Original und mit dem Flex Projector gerechnet; Maßstab 1:800.000, Auflösung 254 dpi. 1 Pixel
am Äquator entspricht etwa 80 km.
Es bedeuten:
Zum Verständnis der RTA-Implementation des Flexprojektors
Mastercode, Recordercode, Fixcode
Der Algorithmus des Flex Projector wurde in 3 verschiedenen Arten in RTA implementiert. Der
Mastercode kann beliebige Koeffizienten rechnen, die jeweils über die Datei
flexi.dat (s. u.) importiert werden. Im Mastercode können also
beliebige Flexprojektionen gerechnet werden.
— Der Recordercode gleicht dem Mastercode,
zeichnet aber zusätzlich die importierten Flexprojektor-Koeffizienten als RTA-Befehlssequenzen auf. —
Unter Fixcode werden
Implementationen verstanden, bei denen die Koeffizienten nicht importiert werden, sondern
als Konstanten unveränderlich im Code stehen. Fixcodeprogramme sind also Flexprojektionsprogramme,
bei denen ein bestimmter Entwurf „fest verdrahtet“ ist. Mit einem Fixcodeprogramm
kann man immer nur eine einzige Flexprojektion rechnen.
Die Übernahme der Koeffizienten über die Datei flexi.dat („Flex Projector Interface“)
Die Übernahme der Koeffizienten des Flex Projector in die Mastercode- oder
Recordercode-Assemblerprogramme erfolgt, indem man die Projektion aus dem Flexprojektor heraus per
File/Save as unter festen Dateinamen
flexi.dat im
dann aktuellen Verzeichnis von RTA bzw. Vimage abspeichert. Diese Interfacedatei flexi.dat wird
automatisch vom Mastercode bzw. vom
Recordercode eingelesen.
Einige Beispiele für die flexi.dat-Dateien:
Interfacedatei
Flexprojection A4 (In flexi.dat umnennen)
Die flexi.dat-Dateien sind immer 86 Zeilen lang. Die Zahlenwerte werden über die
Zeilennummer zugeordnet. Die Dateistruktur entstammt dem Flex Projector, Ausgabe 0.101 beta.
Wenn die Datei flexi.dat nicht gefunden wird, werden alle Koeffizienten auf Null gesetzt,
was in der Regel ein leeres Blatt ergibt.
Ich bedanke mich bei Bernhard Jenny für seine Unterstützung beim Entwurf dieser Schnittstelle.
Wie wird interpoliert?
Newton oder Splines
Eine durch Stützstellen vorgegebene Funktion ist zwar an den Stützstellen eindeutig gegeben. Da es
aber verschiedene Verfahren gibt, mit denen zwischen den Stützstellen interpoliert werden kann,
ist der Verlauf zwischen den Stützstellen nicht ganz eindeitig. Wie groß sind die möglichen Unterschiede?
Hierfür wurde der Recordercode außer in seiner Standardvariante in 2 sog. X-Versionen
implementiert. Die X-Newtonversion rechnet den gleichen Algorithmus, wie die Standardversion
(nur etwas langsamer), nämlich
mit Newtonschen aufsteigenden Differenzen 2. Ordnung. Die X-Splineversion rechnen hingegen mit
kubischen Splines.
Im Ergebnis konnte festgestellt werden, dass das Interpolationsverfahren praktisch keinen Einfluss
auf die Kartengeometrie hat (sofern man nicht ausgerechnet linear interpoliert). Die Unterschiede bewegen sich gewöhnlich im Subpixelbereich.
Hier die Assemblerprogramme der Netze:
Mastercode und Recordercode
Mit diesen Programmen lassen sich beliebige Flexprojektionen herstellen
Flexprojector (Mastercode) (Direkttransformationprogramm)
Fixcodes der neu entwickelten Flex Projections
A4 Projection (Direkttransformationprogramm)
Fixcodes der Approximationen bekannter Kartennetzentwürfe
Aïtoff (Flex Projection) (Direkttransformationprogramm)
Ich bedanke mich herzlich bei Bernhard Jenny für das zur Vefügung gestellte Material.
Passt recht gut
Passt recht gut ...
Passt fast pixelgenau
Passt fast pixelgenau
Grob übereinstimmend
Passt recht gut
Passt pixelgenau
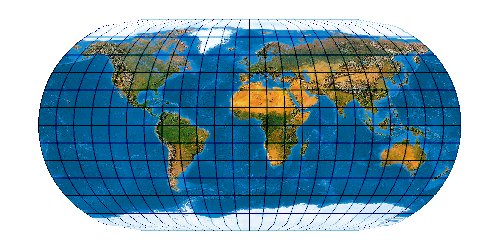Bis Breite 85° pixelgenau, darüber etwas eckig
Passt fast pixelgenau
Passt pixelgenau
Passt fast pixelgenau
Grob übereinstimmend
Passt pixelgenau
Passt pixelgenau
Recht gut übereinstimmend
Passt fast pixelgenau
Passt fast pixelgenau
Pixelgenau
Passt recht gut
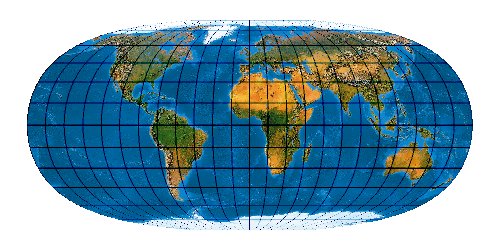Keine Originalrechnung vorhanden. (Visuell ähnlich dem Sine No.1)
Passt pixelgenau
Passt sehr gut.
Passt fast pixelgenau
Passt fast pixelgenau
Passt fast pixelgenau
Passt fast pixelgenau
Passt fast pixelgenau
Passt pixelgenau
Passt pixelgenau
Passt (natürlich) pixelgenau.
Passt gut, bis auf in Polnähe
Passt pixelgenau
Passt pixelgenau
Pixelgenau übereinstimmend
Passt recht gut
Passt fast pixelgenau
Pixelgenau übereinstimmend
Einigermaßen übereinstimmend
Einigermaßen übereinstimmend.
Interfacedatei
Flexprojection Natural Earth (In flexi.dat umnennen)
Interfacedatei
Flexprojection Aïtoff (In flexi.dat umnennen)
Interfacedatei
Flexprojection Quadratische Plattkarte (In flexi.dat umnennen)
Interfacedatei
Flexprojection Mercator-Sanson (Sinusoidal) (In flexi.dat umnennen)
Interfacedatei
Flexprojection Mollweide (In flexi.dat umnennen)
Interfacedatei
Flexprojection Wagner VII (In flexi.dat umnennen)
Interfacedatei
Flexprojection Winkel Tripel (In flexi.dat umnennen)
Flexprojector (Recordercode) (Direkttransformationprogramm)
Flexprojector (Recordercode), X-Newtonversion (Direkttransformationprogramm)
Flexprojector (Recordercode), X-Splineversion (Direkttransformationprogramm)
Natural Earth Projection (Direkttransformationprogramm)
Boggs Eumorphic (Flex Projection) (Direkttransformationprogramm)
Cylindrical Equal-area (Flächentreuer Zylinderentwurf) (F. P.) (Direkttransformationprogramm)
Cylindrical Equidistant (Abstandstreuer Zylinderentwurf oder quadratische Plattkarte) (F. P.) (Direkttransformationprogramm)
Denoyer (Semi Elliptical) (F. P.) (Direkttransformationprogramm)
Eckert-Greiffendorf (F. P.) (Direkttransformationprogramm)
Eckert I (F. P.) (Direkttransformationprogramm)
Eckert III (F. P.) (Direkttransformationprogramm)
Eckert IV (F. P.) (Direkttransformationprogramm)
Eckert V (F. P.) (Direkttransformationprogramm)
Fahey (F. P.) (Direkttransformationprogramm)
Foucaut (F. P.) (Direkttransformationprogramm)
Foucaut Sinusoidal mit n = 0,5 (F. P.) (Direkttransformationprogramm)
Gall Stereographic (F. P.) (Direkttransformationprogramm)
Ginsburg VIII (F. P.) (Direkttransformationprogramm)
Goode Homolosine (F. P.) (Direkttransformationprogramm)
Kavraiskiy V (F. P.) (Direkttransformationprogramm)
Kavraiskiy VII (F. P.) (Direkttransformationprogramm)
Larrivèe (F. P.) (Direkttransformationprogramm)
McBryde-Thomas Flat-Polar Sine (No. 2, F. P.) (Direkttransformationprogramm)
Mercator-Sanson (Sinusoidal) (F. P.) (Direkttransformationprogramm)
Miller Cylindrical (No. 1, F. P.) (Direkttransformationprogramm)
Mollweide (F. P.) (Direkttransformationprogramm)
Nell-Hammer (F. P.) (Direkttransformationprogramm)
Putnins P1 (F. P.) (Direkttransformationprogramm)
Putnins P4 (F. P.) (Direkttransformationprogramm)
Putnins P'4 (F. P.) (Direkttransformationprogramm)
Putnins P'5 (F. P.) (Direkttransformationprogramm)
(Adams) Quartic Authalic (F. P.) (Direkttransformationprogramm)
Robinson-Projektion (F. P.) (Direkttransformationprogramm)
Van der Grinten I (F. P.) (Direkttransformationprogramm)
Wagner II (F. P.) (Direkttransformationprogramm)
Wagner III (F. P.) (Direkttransformationprogramm)
Wagner VI (F. P.) (Direkttransformationprogramm)
Wagner VII (F. P.) (Direkttransformationprogramm)
Werenskiold I (F. P.) (Direkttransformationprogramm)
Winkel I (F. P.) (Direkttransformationprogramm)
Winkel II (F. P.) (Direkttransformationprogramm)
Winkel Tripel (F. P.) (Direkttransformationprogramm)
