
Karlheinz Wagners Buch Kartographische Netzentwürfe, 1. Auflage Leipzig 1949, ist mein Lieblings-Kartennetzentwurfsbuch.
Mir gefällt der Wagner vor allem deshalb, weil man hier nicht in Myriaden von Netzentwürfen „ertränkt“ wird, wovon 95 % völlig ungebräuchlich sind, und die größte Mühe darin besteht, das Wesentliche vom Unwesentlichen zu trennen.
Im Wagner steht alles Wichtige. Mehr ist nicht nötig.
Wagner ist kein ausgesprochener Neuentwickler von Netzentwürfen. Seine Bemühungen gehen eher dahin, vorhandene Netze, wie Mercator-Sanson oder Aïtoff auszubauen, sie z. B. mit Pollinien zu versehen.
John P. Snyder hat Karlheinz Wagner ein schönes Denkmal gesetzt, indem er diese Weiterentwicklungen als Wagner I bis Wagner IX zitiert.
Tauschanzeige: 1962 gab es eine Zweitauflage des Wagner, mittlerweile von Leipzig nach Mannheim übergesiedelt. Ich suche für meine Bibliothek noch ein derartiges 1962er „Mannheimer Exemplar“ und biete dafür ein Expl. der Erstauflage.
Hinter Wagner I bis IX steckt System:
- Wagner I, II, III stammen von Mercator-Sanson ab
- Wagner IV, V, VI sind Mollweide-Weiterentwicklungen
- Wagner VII, VIII und IX sind von querachsigen Azimutalentwürfen abgeleitet
- Wagner I, IV, VII sind flächentreu
- Wagner II, V, VIII sind „flächenreguliert“
- Wagner III, VI, IX sind „abstandsgleich“
Leider erscheinen die 9 Entwürfe nur ganz selten in zusammenhängenden Darstellungen, weshalb ich sie vollständig implementiert habe.
Wie man Wagners Kartennetze rechnet? Hier eine Seite mit den Formeln einschließlich ihrer Inversionen (englisch), für deren Anregung ich mich bei Adrian Weber, ETH Zürich bedanke.
Wagner I, II und III haben den Mercator-Sanson als Stammvater und von diesem dessen sinuslinige Meridiane geerbt.
Unechtzylindrischer flächentreuer Entwurf mit sinuslinigen Meridianen [Entwurf 18a]
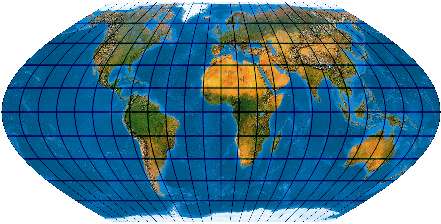
Der Entwurf wurde erstmalig im Schwedischen Nordisk Världatlas 1926 von Karl Rosen angewendet, undabhängig voneinander in der heute gebräuchlichen Form von Wagner (1932) und Kavrayskiy IV (1936) entwickelt, andere Zitate Siemon (1937), Werenskjod (1944). Offenbar lagen in den dreißiger Jahren des 20. Jahrhunderts diese Entwürfe „in der Luft“. [Bei Wagner selbst trägt der Entwurf die Nummer 18a]
Unechtzylindrischer Entwurf mit sinuslinigen Meridianen mit Pollinie und vorgeschriebener Flächenverzerrung [Entwurf 18b]
Wagner II könnte man auch als „flächenreguliertes“ Pendant zu Wagner I auffassen.
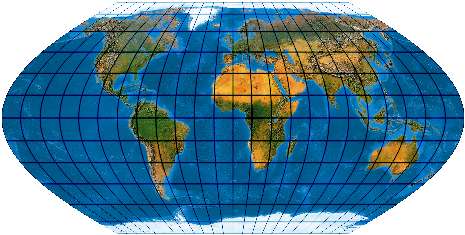
Das Netz ist eine Antwort auf die (geographische) Forderung nach Flächentreue und die (kartographische) Forderung nach guter Formenwiedergabe. Die Flächenverzerrung wird so reguliert, dass sie bis zu einer Breite von 60° 20 % nicht überschreitet. So erhalten die Pole ein klein wenig mehr Raum und werden etwas weniger zusammengedrückt.
Abstandsgleicher unechtzylindrischer Entwurf mit sinuslinigen Meridianen und Pollinie [Entwurf 18c]
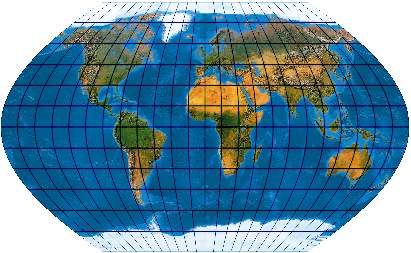
Hier wird die Flächentreue ganz aufgegeben und es werden Meridiane und Parallelen gleichabständig geteilt. Indem man nun statt des Äquators einen bestimmten Längenkreis (hier 45°) längentreu abbildet, erhält man eine bessere Verteilung der Verzerrungen.
Wenn es statt Sinuslinien Ellipsenbögen sein sollen, dann muss Stammvater Mercator-Sanson durch Mollweide ersetzt werden. So entstehen Wagner IV, V und VI.
Flächentreuer unechtzylindrischer Entwurf mit elliptischen Meridianen mit Pollinie [Entwurf 19a]
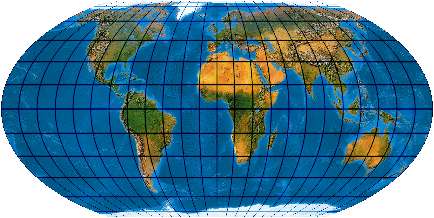
Unechtzylindrischer Entwurf mit elliptischen Meridianen mit Pollinie und vorgeschriebener Flächenverzerrung [Entwurf 19b]
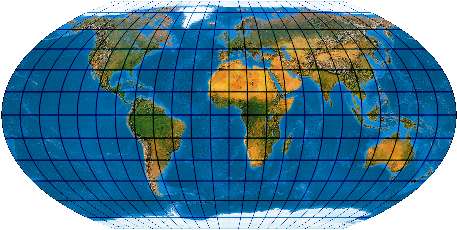
Wie bei Wagner I/II lässt sich auch hier an Stelle der strengen Flächentreue etwas liberaler lediglich eine „Flächenregulierung“ fordern. Die Pole erhalten geringfügig mehr Platz.
Abstandsgleicher unechtzylindrischer Entwurf mit elliptischen Meridianen und Pollinie [Entwurf 19c]
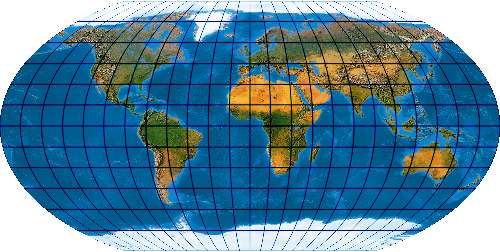
Der in Nullmeridian und Äquator abstandstreue Kollege. Weil das Netz nicht völlig abstandstreu ist, spricht Wagner lediglich von „Abstandsgleichheit“. Auch als Putnin P1 (1934) bekannt. Ähnlich: Kavrayskiy's elliptical pseudocylindrical projection Bugayevskiy, Snyder (1998), S. 77
Eine kleine Geschichte 57 Jahre nach der Veröffentlichung des Wagner VI: Die Originalformel des Entwurfs lautet, wie man auf S. 197 nachlesen kann ...
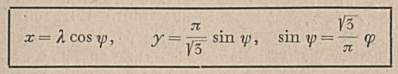
Nun: Ein einfaches y=φ hätte es auch getan, Herr Wagner. Entdeckt von Michael Klein, Berlin, www.kleinplanet.de (Vielen Dank für die Mail vom 10.02.2006 12:08). Ich erhalte den Dienst nach Vorschrift-Preis der Woche, denn ich hatte tatsächlich einen Multiplikationsbefehl abgelocht, und drei Befehle weiter eine Division durch denselben Wert.
(Man schreibt als Ingenieur ja auch ln(e) + sin2(p) + cos2(p) = Σ(½)n und nicht 1 + 1 = 2.)
Mit Wagner VII, VIII und IX vollendet sich das System. So wie ihre Vorgänger von Mercator-Sanson und Mollweide abgeleitet sind, so haben diese drei Entwürfe querachsige Azimutalantwürfe zu Stammvätern. Damit werden sie zugleich Weiterentwicklungen des Hammerschen Entwurfes, der ja eine Transformation des querachsigen flächentreuen Azimutalentwurfes darstellt und des Aïtoff, dem transformierten querachsigen abstandstreuen Azimutalentwurf.
Hammerscher Entwurf mit Pollinie (flächentreu) [Entwurf 20b]
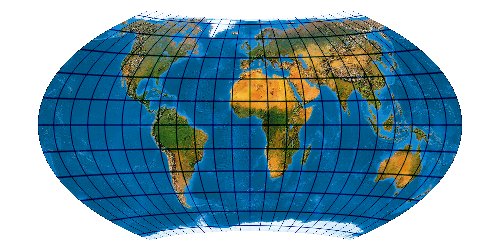
Mit seinen geschwungenen Netzlinien ein wunderbar ästhetisches Netz, das fast so gut wie der Winkel Triple abbildet darüber hinaus aber flächentreu ist. 1941 im Jahrbuch der Kartographie erstmals vorgestellt. Auch als Hammer-Wagner zitiert.
Hammerscher Entwurf mit Pollinie und vorgegebener Flächenverzerrung [Entwurf 20c]

Mit einer begrenzt zugelassenen Flächenverzerrung kann man die Formwiedergabe noch verbessern. Wagner VIII ist eines der schönsten Kartennetzentwürfe überhaupt.
Hier die Karte als Großformat (200 kByte) im Maßstab 1:200.000.000 (bei 254 dpi)
Aïtoffscher Entwurf mit Pollinie [Entwurf 21b].
Indem nunmehr Aïtoff eine Pollinie hinzufügt vollendet sich das System.
Hier versucht Wagner direkt eine „Winkel-Simulation“. Es entsteht ein Netz
und ein Erdbild, welches hinsichtlich Schönheit und Verzerrungsarmut
Wagner VIII ebenbürtig ist. Auch als Aïtoff-Wagner zitiert.
Wir folgen streng Wagners Formel, so auch G. I. Evenden. Wagners Abbildung 105
hingegen zeigt das Netz mit einem Faktor a = 0,88 in X-Richtung gestaucht und gibt eine Erläuterung im Text
(Wagner (1949) S. 215). Dies ist auch die Lesart des Wagner IX von F. Canters (2002).
Wir verzeichnen letztere Varinte als
Wagner Y5.
Darüberhinaus gibt es noch einige weitere kleinere Entwicklungen von Wagner:
Wagner Y1 (Eckert-IV authentisch)
Assemblerprogramme:
Wagner I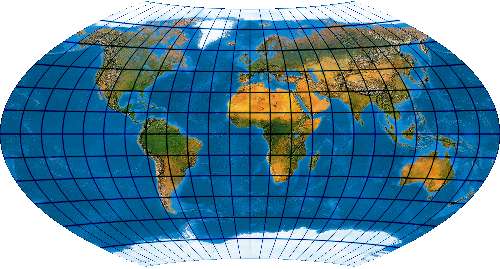
Wagner Y2 (Eckert-IV mit 2 längentreuen Parallelkreisen)
Wagner Y3 (Van der Grinten-Adaption 1)
Wagner Y4 (Van der Grinten-Adaption 2)
Wagner Y5 (Wagner IX nach Wagners Abbildung 105, mit Faktor a = 0,88)
Wagner II
Wagner III
Wagner IV
Wagner V
Wagner VI
Wagner VII oder Hammer-Wagner
Wagner VIII
Wagner IX oder Aïtoff-Wagner
Zum Schluss: Wagner hat einen weiteren Vorteil, der sich
für den ihm insbesondere der Programmierer dankbar sein kann:
Die Setzer am Blei haben früher weniger geschusselt, als heute
die Autoren am Computer. So habe ich bisher in den über 250 Seiten nur 4 ½
Satzfehler gefunden: