Hier eine Auswahl (heute) seltener gebräuchlicher oder schwer zu klassifizierender Kartennetze.
[Evenden (2005): 8.1.6]
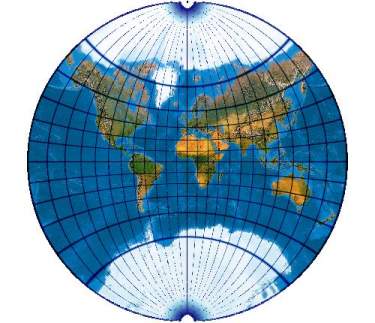
In der amerikanischen Literatur sehr beliebt sind die Projektionen van der Grintens. Hier wird die gesamte Welt in einer Kreisfläche abgebildet. Der gewöhnliche Van der Grinten oder Van der Grinten I:
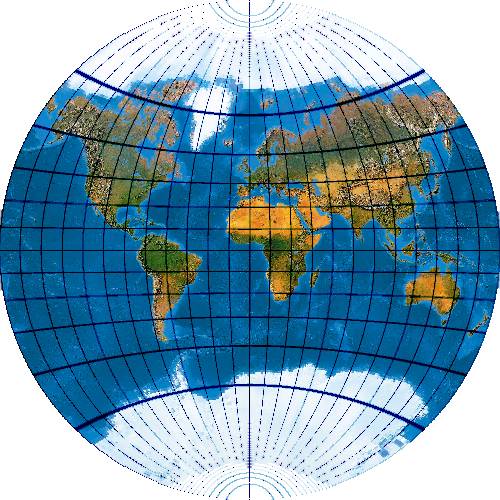
Wagner empfiehlt statt den Van der Grinten zu rechnen, andere Netze geeignet umzubeziffern.
Der Y3 ist eine Umbezifferung des querachsigen winkeltreuen Azimutalentwurfes, hier mit Grenzparallel 45° und Grenzmeridian 90°.
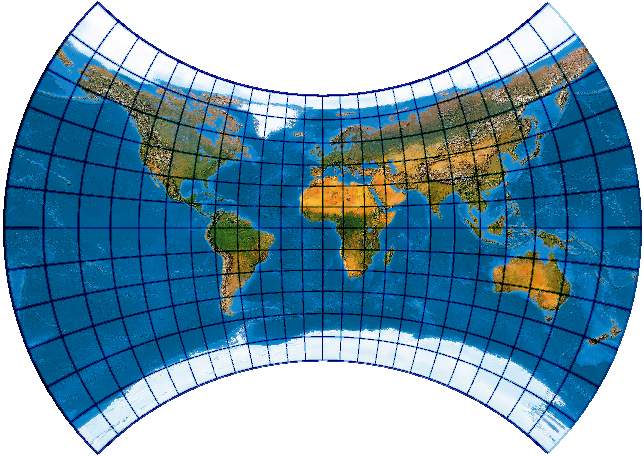
Der Y4 nutzt für die Meridiane statt dessen den querachsigen abstandstreuen Azimutalentwurf, Parallelkreisformel wie "Y3".
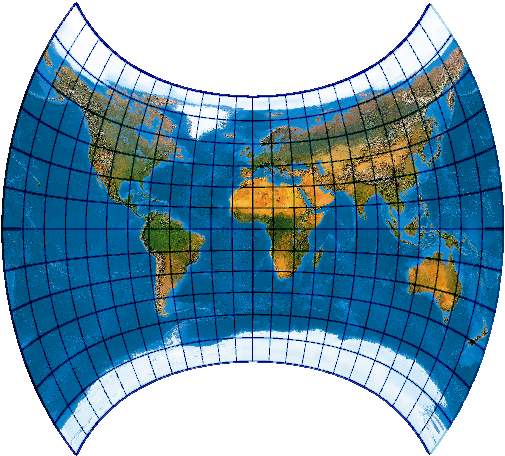
Man entdeckt diese Netze nur bei sehr aufmerksamer Lektüre des "Wagner" auf S. 227. Es darf vermutet werden, dass dies die erste Implementation dieser Netze ist. Auf S. 228 oben wird noch ein weiteres Netz vorgeschlagen.
(Wagner bezeichnet diese Netze nicht gesondert, weswegen sie hier (wie auch Y1 und Y2) als Y3 und Y4 gezählt werden.)
Der Wagner IX nicht nach Wagners Formel, sondern nach Wagners Zeichnung ...
Es ist nicht völlig eindeutig, um welchen Netzentwurf es sich bei dem
Wagner-Aïtoff (dem Wagner IX) eigentlich handelt.
Der originale Wagner IX wird durch die
von Wagner angegebenen Formeln konstituiert. So wird er auch von Evenden zitiert.
Wagners Abbildung zeigt aber einen um einen Faktor
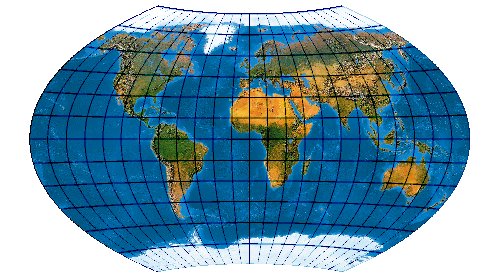
Ein winkeltreuer Netzentwurf
Der Nurflügler unter den Kartennetzen: Collignon bildet die ganze Welt in einem Dreieck ab ...
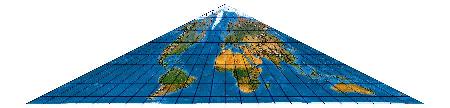
(Maßstab [bei 254 dpi] 1 : 1.600.000.000)
... was natürlich auch andersherum geht:
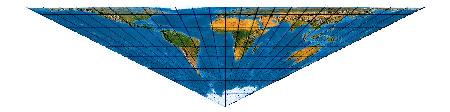
(Maßstab [bei 254 dpi] 1 : 1.600.000.000)
[Evenden (2005): 5.2.23]
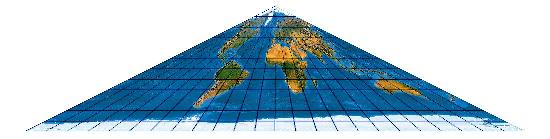
(Maßstab [bei 254 dpi] 1 : 1.600.000.000)
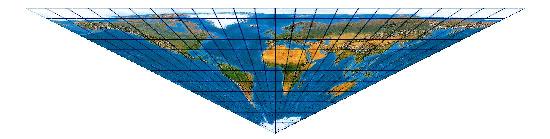
(Maßstab [bei 254 dpi] 1 : 1.600.000.000)
[Evenden (2005): 5.2.43]
Ein bemerkenswerter Netzentwurf, übrigens winkeltreu ...
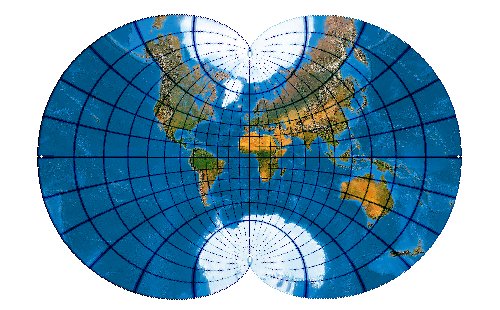
(Maßstab [bei 254 dpi] 1 : 1.600.000.000)
[Evenden (2005): 8.1.4]
Ebenfalls winkeltreu.
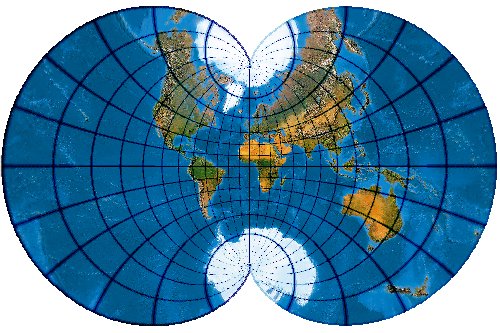
(Maßstab [bei 254 dpi] 1 : 1.600.000.000)
[Evenden (2005): 8.1.5]
Noch ein winkeltreues Netz: Littrows Projection. Am „Ost-“ und „Westpol“ zerfällt die Kartenebene in zwei Blätter, was mich ein wenig an Riemann erinnert. — Zitiert im Bugayevskij/Snyder (1998) auf S. 205ff. Hier eine Karte mit dem Mittelmeridian 60° Ost.

Von der Netzentwurfentwicklung allein konnte Ernst Hammer nicht leben. Zum Broterwerb verfasste er u. a. Der logarithmische Rechenschieber und sein Gebrauch (Stuttgart 1889). Ausserdem arbeitete an der Entwicklung von Heizrohrsystemen mit ...
Ein bemerkenswertes Netz, das sich u. a. auf der Schmutztitel-Rückseite des Synder & Voxland (1989) abgebildet ist. Hier eine mit Berührungsbreite 30° gerechnete Projektion.

Hier der Craig, so wie er im Snyder & Voxland (1989) vorgestellt wird: Zentralpunkt 38.5° N -90° W. (Wahrscheinlich kommen Snyder und Voxlnd aus St. Louis.) Weil das Netz ziemlich klein läuft, hier Maßstab 1:400.000.000 statt 1:800.000.000 (bei 254 dpi).
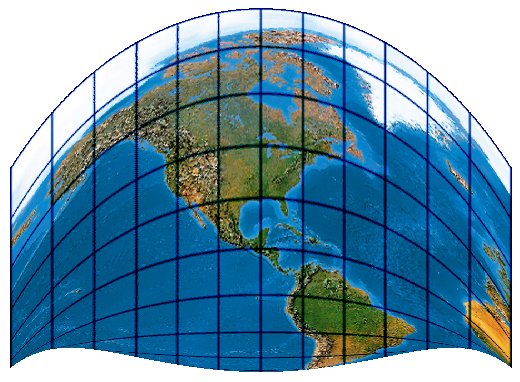
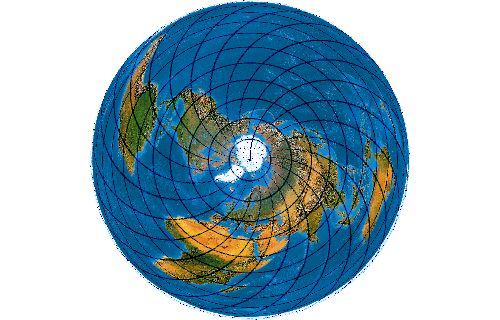
[Bugayevskiy/Snyder (1998): S. 132]
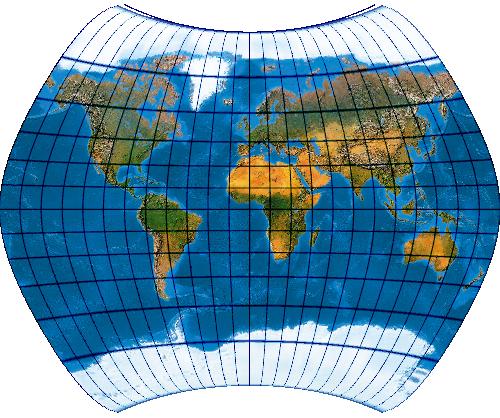
[Evenden (2005): 8.1.14]
Netze programmieren klappt nicht immer auf Anhieb. Einen Tag vor dem 14. Geburtstag meiner Tochter Freia erhielt ich zufällig zwei Mails, eine von Janos Györffy und eine von Gerald I. Evenden, die mich beide veranlassten wieder einmal ein paar Netze zu schreiben. Ich entschied mich zunächst für den Fournier Globular I, implementierte aber zunächst mit drei Fehlern. Nun hatte sich Freia schon immer eine ganz besondere Weltkarte gewünscht ...
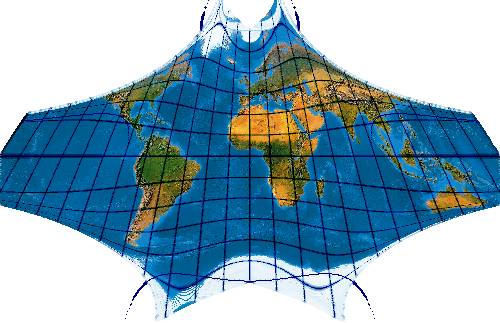
Nicht bei Evenden verzeichnet. Index 8.1.6 ist der Fournier Globular I.
Assemblerprogramme:
Von diesen seltener oder kaum gebräuchlicheren Netzentwürfen habe ich meist nur eine Direkttransformation programmiert.
Direktprogramm heisst, dass nicht die für ein übliches Resampling erforderliche Inversformel programmiert wurde, sondern die (meist in der Literatur ausschliesslich angegebene) Forewardformel.
Damit sind die Programme für ein Resampling ungeeignet. Man kann sie aber mit dem Vimage-Direkttransformator rechnen. Hierzu gehört aber etwas Übung.
Van der Grinten-Projektion I (Direktprogramm)
Wagner Y3 (Van der Grinten-Adaption 1) (Direktprogramm)
Wagner Y4 (Van der Grinten-Adaption 2) (Direktprogramm)
Wagner Y5 (Der Wagner IX nicht nach Wagners Formel, sondern nach Wagners Abbildung) (Direktprogramm)
August Epicycloidal (Direktprogramm)
Eisenlohr (Direktprogramm)
Littrow (Direktprogramm)
Hammer Retroazimuthal (Direktprogramm)
Craig Retroazimuthal (Direktprogramm)
Wiechel Pseudoazimuthal (Direktprogramm)
Larrivée (Direktprogramm)
Freias Birthday (Direktprogramm)