Eine Motivationsseite für alle, die schonmal durch eine Matheprüfung gefallen sind
Wie berechnet man den Schwerpunkt einer Fläche?
Jan Sebastian hat mich motiviert, nach dem Mittelpunkt der Sächsischen Schweiz zu suchen und Gerald Schöbl hat mir dazu diesen Link geschickt. Dort gibt es ganz viele Vorschläge, einen „Mittelpunkt“ zu bestimmen. Unmassen Dreiecke, Vierecke, Inkreise, Umkreise usw., und kaum setzt man irgendeinen Punkt anders, kommt ein völlig anderer „Mittelpunkt“ raus. Kein Wunder dass mit den vielen „Mittelpunkten“ von Europa, Deutschland, Sachsen usw. keiner mehr durchsieht.
Klare Ansage: Es gibt immer nur eine einzige Art Mittelpunkt, und das ist der Schwerpunkt. Um diesen zu ermitteln, haben aber alle immer nur den Tipp, Fläche ausdrucken, auf Sperrholz aufkleben, aussägen und dann das Brettchen so lange auf einer Nadelspitze hin- und herbalancieren, bis es „stabil liegt“. Der Nadelaufsetzpunkt ist dann der Schwerpunkt. Irgendwie unpraktisch und – sollte das nicht auch irgendwie ein Computer rauskriegen können?
Klar, Wikipedia, aber, oh Schreck, 1000 Formeln, gigantische Integrale, die keiner kapiert. Mit solcherart mathematischer Wichtigtuerei haben schon ganze Generationen von Schülern und Studenten Mathe hassen gelernt und auf Politologie umgeswitcht.
Geht es nicht digital und einfach zugleich? Muss man immer alles mit so blöden Formeln machen? Muss man nicht, Mathe kann man auch mit ein paar schönen Bildern machen. Ich bedanke mich herzlich bei Thomas Steinbrecher, Hildesheim, der mir zu den folgenden Berechnungen die Grundidee geliefert hat.
Los gehts ...
Als Ausgangsmaterial braucht man ein Bild von dem Gebiet, dessen Schwerpunkt bestimmt werden soll. Die Gebietsabgrenzung haben wir ja bereits hier festgelegt und können diese übernehmen:
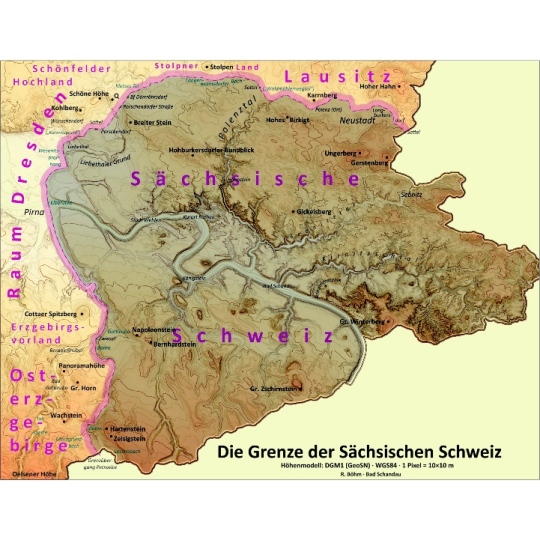
Sächsische Schweiz, volle Auflösung 3600×3600
Aus methodischen Gründen wurde das Bild von 2800×3600 auf Bildgröße „quadratisch 3600×3600“ ergänzt, indem unten/oben je 400 Pixel angefügt wurden. Das Koordinatensystem liegt so, dass
- das Bild quadratisch ist (3600×3600 Pixel/muss nicht sein, ist aber hilfreich).
- Jedes Pixel misst exakt 10×10 Meter, Bildgröße in der Natur damit 36×36 km.
- Alles steht in UTM-Koordinaten. X läuft von links nach rechts und Y von unten nach oben.
- Die Südwestecke liegt auf UTM-Wert 4 22 000; 56 24 000 Meter. Das bitte merken, werden wir noch brauchen.
Aus diesem Bild holen wir nun die „Sächsische-Schweiz-Fläche“ als schönes Schwarz-Weiß-Bild raus:
Rechnerisch bedeutsam ist, dass wir die Pixelgrauwerte nicht, wie in der Bildverarbeitung meist üblich, von 0 bis 255 laufen lassen, vielmehr gilt 0=weiß und 1=schwarz und andere Pixelgrauwerte dürfen in dem Bild nicht vorkommen. Typisch digital also. Damit haben wir ein „Binärbild“ der Fläche, deren Schwerpunkt zu bestimmen ist.
Zuerst müssen wir herausbekommen, wie viele schwarze Pixel es gibt. Unser Rechenknecht Computer zählt diese in einer Zehntelsekunde durch: 5.173.962 Stück. Wichtiger Wert, 5,17 Millionen, bitte ebenfalls merken.
Nun machen wir einen „Keil“, genaugenommen einen „X-Keil“ ...

(X-Keil in 15% Größe)
Ein X-Keil ist ein Bild, in dem alle Pixel der 1. Spalte den Grauwert 1 haben, 2. Spalte Grauwert 2, 3. Spalte Grauwert 3 usw. fort bis zur letzten Spalte. Dort steht in unserem Fall Grauwert 3600. In jedem Pixel steht also dessen X-Adresse.
Nun wird unser Binärbild mit dem Keil multipliziert. Man kann auch sagen, zusammenmaskiert: wo das Binärbild schwarz ist, wird der Keil „durchgepaust“, was weiß ist, bleibt weiß. Als Ergebnis Binärbild × X-Keil entsteht folgendes „X-Messbild“:

(X-Messbild, in 15 % Größe)
In den Sächsischen-Schweiz-Pixeln steht nun also die X-Pixeladresse, Außerhalbgebiete sind weiß, was Null bedeutet.
Nun etwas Mathe, aber nicht schlimm: Das arithmetische Mittel von mehreren Zahlenwerten ist die Summe der Werte geteilt durch Anzahl der Werte.
Das steht so zwar auch in der Wikipedia unter „Geometrischer Schwerpunkt“, aber die schreiben das so:
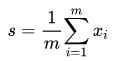
Klar, muss ja kompliziert aussehen. Dazu Garnierung mit einem Geschwubel von „ℝ-Vektorraum“;, „k-dimensionalem Simplex“ und „baryzentrischen Koordinaten“. Da muss man erst einmal draufkommen, dass das alles völlig überflüssig ist.
Und überhaupt, wieso die immer mit so Differential- und Integralrechnung anfangen. Und du denkst dann immer, wow, das kapier ich nie. Andersherum wird eine Schuh daraus. Es ist doch völlig klar, dass es in Wirklichkeit so etwas, wie diese „unendlich kleinen“ Differentiale gar nicht geben kann. Eben weil „unendlich klein“ niemals zu kapieren ist. Das kapiert übrigens auch kein Computer, eine reele Zahl, ein „unendlich kleines bisschen größer“ als Null. Computer können immer nur rationale Zahlen. „Unendlich klein“ über Null geht überhaupt nicht. Die allerkleinste Zahl größer als Null (die ein Programmierer in „double“ definieren kann), ist ungefähr 10-308. Das ist keinesfalls „unendlich klein“, sondern vielmehr „endlich klein“ (wenn auch vielleicht „winzig klein“). Genauso ein Pixel. Das ist auch nicht „unendlich klein“, sondern „endlich klein“ und damit begreifbar. Da weiß man, was man hat. Entschuldigung, kleine Abschweifung.
Zurück zum Thema. Arithmetisches Mittel. Summe der Werte geteilt durch Anzahl der Werte.
Vom Messbild kann man nun ein Histogramm machen und die „Pixelsumme“ ermitteln, das sind alle Pixel zusammengerechnet. Die Pixelsumme unseres X-Messbildes lautet 8.826.090.229.
Die Pixelanzahl hatten wir bereits oben anhand des Binärbildes ermittelt und uns gemerkt. Das waren die 5,17 Millionen. Nun Rechnung 8.826.090.229 geteilt durch 5.173.962 ergibt 1705,8668. Genau das ist die X-Adresse des gesuchten Schwerpunktes. So einfach ist das. Teil 1 – erledigt.
Teil 2 ist Y. Dasselbe nochmal. Nun nehmen wir einen Y-Keil ...

(Y-Keil in 15 % Größe)
... multiplizieren den mit dem Binärbild, und erhalten nun das „Y-Messbild“:

(Y-Messbild in 15 % Größe)
Auch hier wieder Pixelsumme bestimmen, unsere Bildverarbeitung ermittelt 9.777.457.095. Das wieder durch die Pixelanzahl teilen, also 5.173.962, Ergebnis 1889,7427; das ist die Y-Adresse. So einfach ist das also:
X=1705,8668; Y=1889,7427
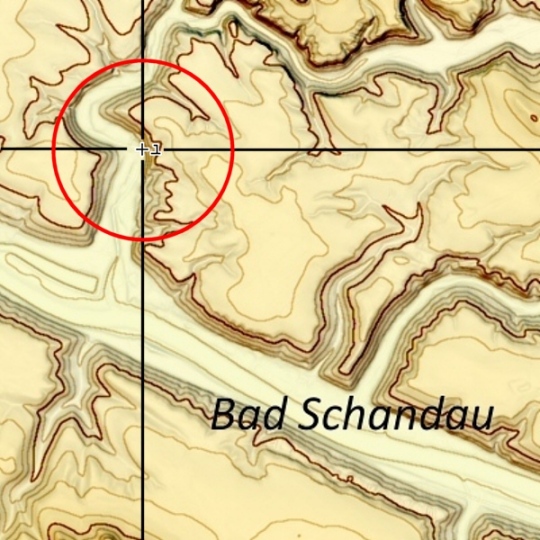
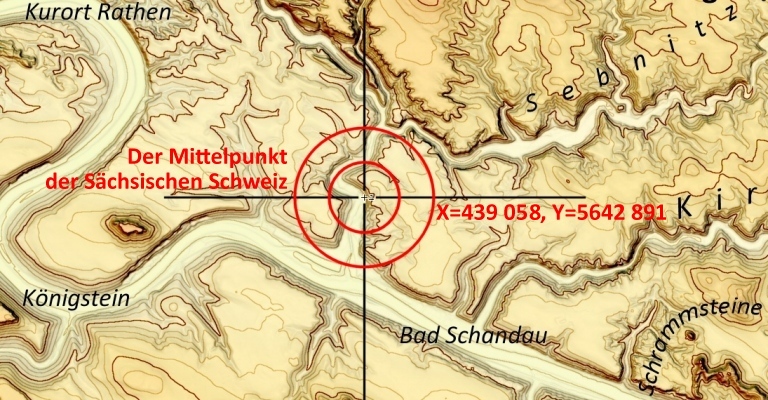
Fertig. Nun können wir den Mittelpunkt schonmal in das Bild einplotten:
So, das ist eigentlich alles.
Probe
Stimmt das Ergebnis aber auch? Könnte ja sein, wir haben uns verrechnet oder alles ist falsch. Darum Verprobung.
Es ist eine Grundeigenschaft des Schwerpunktes, koordinatenunabhängig zu sein. Wir drehen unser Bild um 30°. Neues Koordinatensystem, erneute Schwerpunktberechnung. (8660913376/5174002=1673,9 und 9470893416/5174002=1830,5. Wer sich über die andere Pixelzahl wundert, die hat sich beim Verdrehen von 5173962 auf 5174002 geändert). Völlig andere Bildkoordinate ...
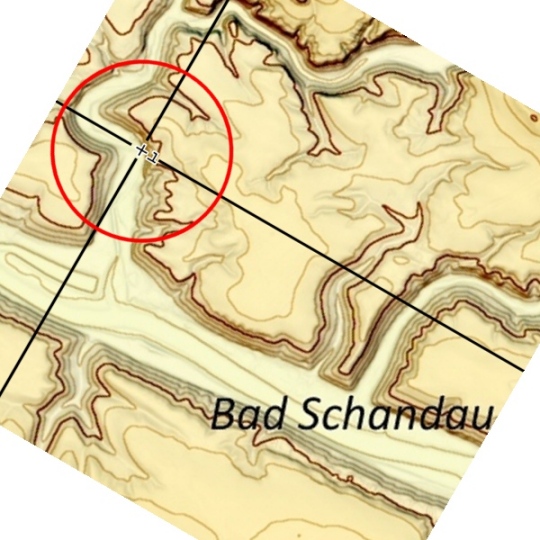
Gesamtbild um 30º verdreht, mit Schwerpunkt
... aber der Schwerpunkt liegt an genau derselben Stelle in der Landschaft. Noch ein Versuch, Drehung um insgesamt 60°, wieder neue Schwerpunktberechnung ( ... 1675,9; 1763,2):
Gesamtbild um 60º verdreht, mit Schwerpunkt
Man kann machen, was man will, der Schwerpunkt bleibt immer an derselben Stelle.
Offenbar stimmt alles und der ermittelte Punkt ist wirklich der Schwerpunkt der Sächsischen Schweiz.
Ergebnis
Noch sind wir nicht ganz fertig. Für einen ordentlichen Mittelpunkt geziemt es sich, dass seine Koordinaten korrekt in UTM angegeben werden. Also Bildadressen X=1705,8668; Y=1889,7427 mit Pixelgröße 10 Meter multiplizieren und UTM-Adresse der linken unteren Bildecke dazurechnen:
---------------------------------------------------------
X Y
---------------------------------------------------------
SW-Bildecke UTM 422000,000 5624000,000
+ Bildkoordinate Schwerpunkt 17058,668 18897,427
= Koordinate Schwerpunkt UTM 439058,668 5642897,427
---------------------------------------------------------
Werte ein wenig gerundet und unter Berücksichtigung der Berechnungen von Maik Nicke (s. u.), ausgeglichen:
X=439058, Y=5642891
Hier noch die Umrechnung in Grad (WGS84):
50° 56' 4" 14° 7' 58" (Grad, Minute, Sekunde) 50° 56,065' 14° 7,963' (dezimalgeteilte Minute) 50,93443 14,13272 (Dezimalgrad) 50934430 14132720 (Mikrograd)
Und wo liegt nun der Mittelpunkt der Sächsischen Schweiz im Gelände? In Rathmannsdorf, s. hierzu unten, Nachtrag vom 19.01.2021: Der Punkt liegt 114 Meter unterhalb der Mittelachse der Eisenbahnbrücke vor dem Mühlhorntunnel (die gerade neu errichtet worden ist). Vom der Südostecke des letzten Nebengebäudes bergseitig (einem Carport) sind es 51 Meter. Entfernung von der Straßenachse 6 m (also vielleicht 3 m ab Mauer im Gelände).
Anmerkungen
- Datenquelle ist das wunderbare DGM1 von GeoSN, vormals Landesvermessungsamt Sachsen. Wenn das noch die alten Topographen um Uli Ruske wüssten. Die sind früher monatelang mit Theodolit und Dahlta-Latte durch das Gelände gesaust und Günther Oehmichen hat die Höhenlinien konstruiert. Alles von Hand. Jaja, so was das eben – früher.
- Die Landesgrenze wurde 1:1 aus der Datenquelle DGM1 übernommen, stimmt dort aber nicht ganz. Die Daten ragen nämlich etwa 120 Meter nach Tschechien hinein. Darum habe ich an der Landesgrenze 12 Pixel mit dem Minimumfilter wegmaskiert. Anhand der Höhenlinien (die Grenze verläuft oft in Tallinien) kann man ganz gut erkennen, dass das bis auf 1 bis 2 Pixel Restfehler ganz gut funktioniert.
- Das Interessante an dem Verfahren ist, dass ihm egal ist, ob das Gebiet Löcher, Inseln (Exklaven oder Enklaven) aufweist. Während diese beim „lehrbuchmäßigen Integrieren“ immer mit extra Separatkurven umständlich sonderbehandelt werden müssen, ist das hier nicht erforderlich.
- Wers das Ganze einmal nachstellen will, braucht die Keile. Hier ein X-Graukeil 4000×4000 und ein Y-Graukeil 4000×4000. (Headerlose Rohdaten, 2 Byte pro Pixel, 4000×4000×2=32000000 Byte, ohne „Essig und Öl“. Als Rohdaten importieren, dabei Bildgröße 4000×4000 angeben und Datentyp 16 Bit Integer. Ob signed oder unsigned ist egal.)
- Die Genauigkeit unseres Umrisses der Sächsischen Schweiz liegt bei etwa ±50 Meter, Lokalisierung des Mittelpunktes im Gelände anhand Karte etwa ±3 m. Das Verfahren der Mittelpunktsbestimmung selbst ist auf vielleicht 0,001 Pixel, also Zentimeter genau.
Nachtrag 13.01.2021
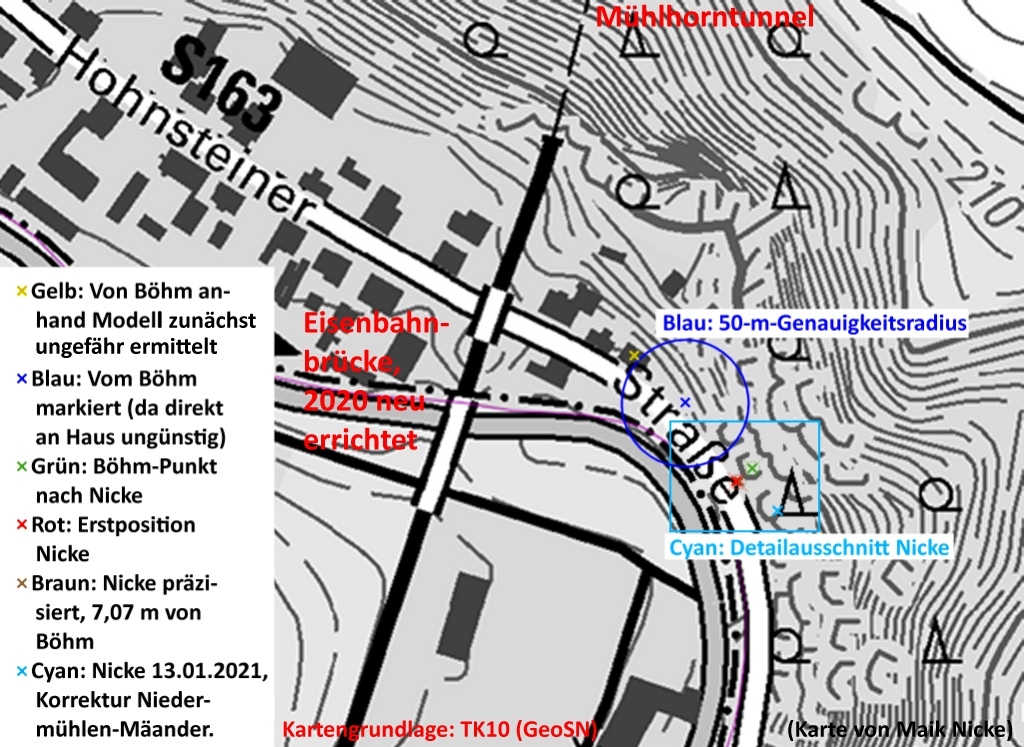
Maik Nicke hat mein Verfahren geprüft und ist zu leicht abweichenden Punktlagen gekommen.
- Gelb ist die von mir anhand der Höhenliniendarstellung zunächst ungefähr ermittelte Punktlage.
- Blau: Weil dies aber in einem Wohngebäude liegt, habe ich den Punkt einfach etwas nach Osten verlegt (weißes Kreuz an einer Trockenmauer).
- Grün: Möglicherweise habe ich mich dabei etwas verschätzt. Maik Nicke lokalisiert meinen Punkt (439058,668; 5642897,427) auf Lage Grün.
- Rot: Am 17.12.2020 hat Maik Nicke die Schwerpunktberechnung wiederholt und nun (439052,900; 5642892,600) ermittelt. Den Restfehler von 7,52 m führe ich zunächst auf eine „gewisse Zeichenungenauigkeit“ zurück.
- Braun (fast unter rot liegend): Eine millimetergenaue Nachrechnung von Maik Nicke vom 23.12.2020 liefert Koordinate (439053,668; 5642892,428). Wenn man nun auch meine Koordinaten millimetergenau ausrechnet, erhält man als Restfehler X 5,000 und Y 4,999 m. Nun sind ja unsere Pixel genau 10 Meter groß. Das klärt die tiefere Ursache der vermeintlichen „Zeichenungenauigkeit“ auf: Da habe ich den Unterschied zwischen Pixelmitte und Pixelecke nicht beachtet. (Es ist dies übrigens eine schöne Illustration, dass das in der Geodäsie übliche, vermeintlich sinnlose Mitführen von Millimeterstellen doch einen Zweck hat.)
-
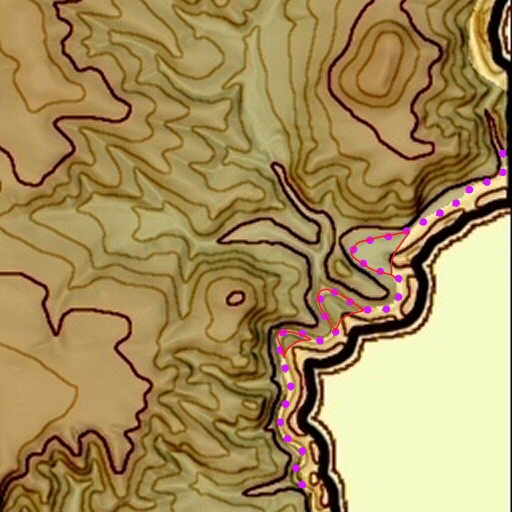
Cyan: Am 13.01.2021 hat Maik Nicke noch eine weiteren Fehlereinfluss ermittelt. Ich habe das etwas über die Grenze reichende Höhenmodell
mit einem Minimumfilter auf die Grenzlinie „zurückgefiltert“ (solange Pixel weggenommen,
bis die Grenzlinie genau in der Muldenlinie der Grenzwasserläufen entlanglief).
Rasterbildverarbeiter wissen: Dabei können Mäander zulaufen. Kleine Mäander stören freilich nicht, große Mäander laufen nicht zu.
Leider gibt es an der Hinterhermsdorfer Niedermühle aber ein paar „mittelgroße“ Mäander und dort hat sich die Grenze etwas systematisch verschoben:
Maik Nicke hat es korrigiert und Schwerpunktlage (439066,100); 5642882,600) gefunden. Versatz zu Grün 14,80 Meter.
So liegen die Punkte in der Örtlichkeit:
Zusammenfassung:
--------------------------------------------------------------------------- Mittelpunkt der Sächsischen Schweiz X Y --------------------------------------------------------------------------- Böhm, 29.12.2019, Lage „grün“ 439058,668 5642897,427 Nicke, 17.12.2020, Lage „rot“ 439052,900 5642892,600 Nicke, 23.12.2020, Lage „braun 439053,668 5642892,428 Nicke, 13.01.2021, Lage „cyan“ 439066,100 5642882,600 Mittelwert 439057,834 ±6,075 5642891,264 ±6,223 Gerundet 439058,000 5642891,000 ---------------------------------------------------------------------------
Ich bedanke mich herzlich bei Maik Nicke für die aufwändige Nachstellung der Koordinatenberechnung.
Nachtrag 19.01.2021
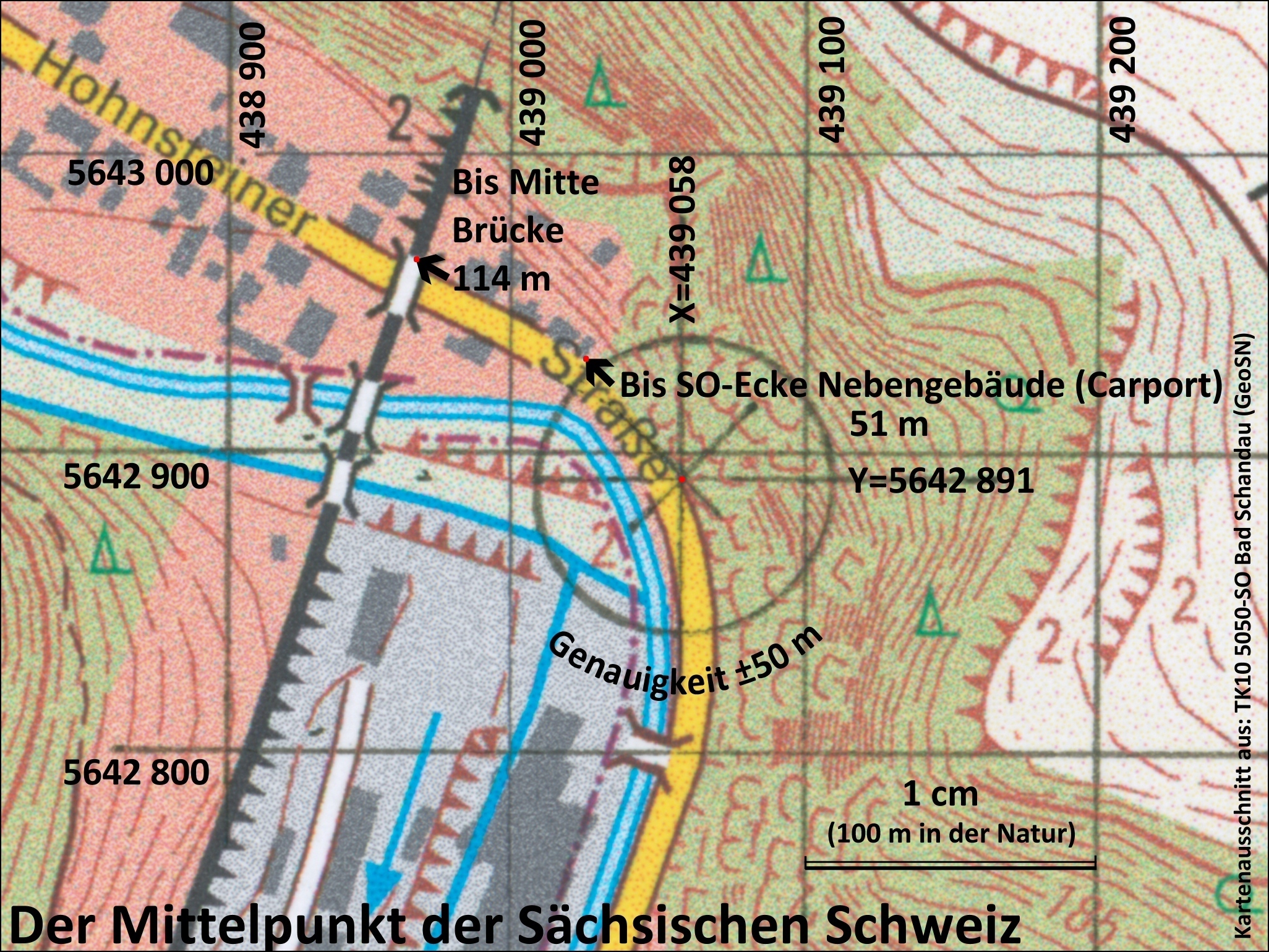
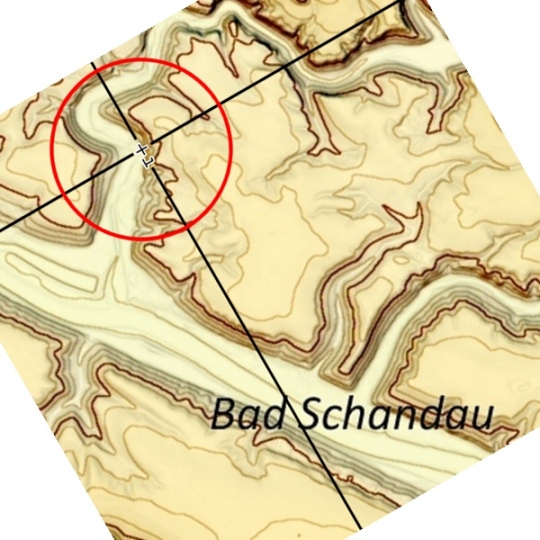
Oh so viele Informationen! Geht es nicht auch einfacher? Natürlich, mit einer guten alte Papierkarte vom Landesvermessungsamt. Einfach mit Zeichendreieck und Tusche alles auf Top. Karte 1:10000 einzeichnen:
Damit lässt sich nun auch die genaue Punktlage im Gelände ermitteln: Der Punkt liegt 114 Meter unterhalb der Mittelachse der Eisenbahnbrücke vor dem Mühlhorntunnel (die gerade neu errichtet worden ist). Vom der Südostecke des letzten Nebengebäudes bergseitig (einem Carport) sind es 51 Meter. Entfernung von der Straßenachse 6 m (also vielleicht 3 m ab Mauer im Gelände).
28.11.2019: Initial
03.12.2019: Rohfertig
29.12.2019: Geprüft und fertig zusammengeschrieben
13.01.2021: Nachprüfung Maik Nicke
19.01.2021: Einzeichnung Top. Karte 1:10000
22.10.2022: Geographische Koordinten hinzugefügt