Verzeichnis aller Canters-Netze. Canters Index Table with all projections
[Frank Canters Eurafrica Projections]
Außer den Weltkartennetzen hat Frank Canters auch eine Reihe von Projektionen entwickelt, die nur einen Teil der Erdoberfläche abbilden.
Der „Eurafrica“-Aufgabe stellte sich erstmals Miller 1953, dann Tobler 1974, schließlich Canters 2002: Abzubildendes Gebiet: Europa und Afrika, Ziel der Abbildung: Flächentreue bei minimalen Winkelverzerrungen. Zunächst wird ein schief gelagerter flächentreuer (Lambertscher) Azimutalentwurf gerechnet ...
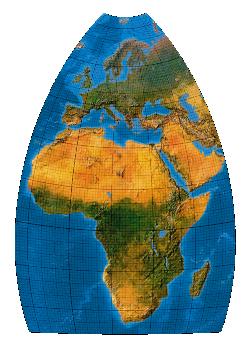
Nun wird dieses Netz mit einer ebenen x-y-zu-x'-y'-Transformation erneut abgebildet. Dabei werden spezielle von Canters entwickelte Polynome zum Einsatz kommen, die die Flächentreue erhalten. Es handelt sich also nicht um Projektionen der üblichen Art (Erde in Karte), sondern um sog. Post-Transformationen einer bereits vorliegenden Karte (Karte in Karte).
First-order transformation with equal maximum scale factor along the two major axes
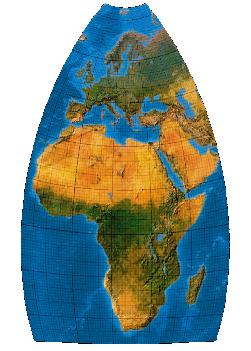
Wenn man den schiefachsigen Lambert nun in X-Richtung (linear) auf 97,5 % staucht und in Y-Richtung (linear) um 97,5 % streckt, so bleibt die Flächentreue erhalten – aber die Winkelverzerrungen werden geringer. So entsteht der ein Netz, das bereits 1974 von Tobler vorgestellt wurde. Dieses Netz stellt den Anfang der Cantersschen Entwicklungen dar und soll deshalb hier als Canters P10 zitiert werden.
Excuse Prof. Tobler: This Graticule is not a Canters, it is a Tobler (1974). But it is the methodicl beginning of the following Canters Projections. For this reason I have classified it here in the Canters index as a P10.
[Canters (2002), p. 227f., Tab. 5.23, Fig. 5.34 (a)]
First-order transformation with minimum mean finite scale factor
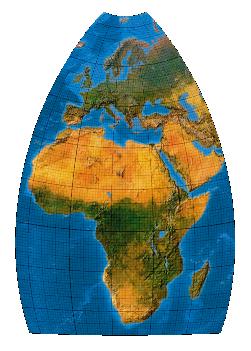
Eine andere von Canters entwickelte lineare Variante
[Canters (2002), p. 227f., Tab. 5.23, Fig. 5.34 (b)]
Third-order transformation with twofold symmetry
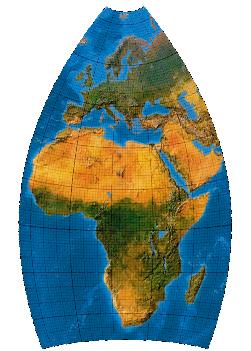
Interessanter wird es, wenn man Streckung und Stauchung als polynomische Transformation 1. Grades auffasst und auf höhere Grade übergeht. Hier Canters kubischer Eurafrica mit zweifacher Symmetrie.
[Canters (2002), p. 227f., Tab. 5.23, Fig. 5.35 (a)]
Third-order transformation with one-fold symmetry
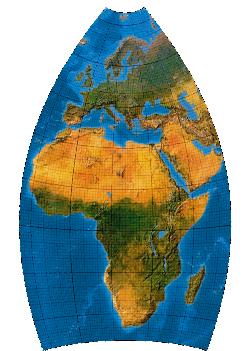
Kubische Polynome, eine Symmetrieachse
[Canters (2002), p. 227f., Tab. 5.23, Fig. 5.36 (a)]
Third-order transformation without symmetry
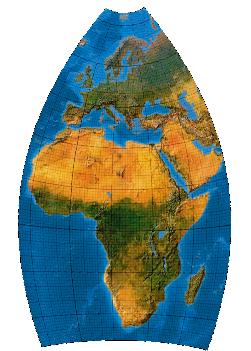
Weil Canters Landflächen-Strecken zur Grundlage seiner Optimierungen macht und die Landflächen im Kartengebiet unsymmetrisch angeordnet sind, ergeben sich die geringsten Verzerrungen (bezüglich der Landflächen), wenn man überhaupt keine Symmetriebedingungen stellt. Kubische Polynome. Völlige Assymetrie.
[Canters (2002), p. 227f., Tab. 5.23, Fig. 5.37 (a)]
Fifth-order transformation with twofold symmetry
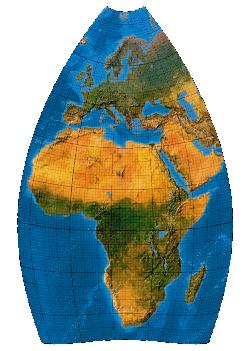
Der gewellte Kartensüdrand offenbart Polynome höheren Grades. Canters Eurafrica-Netz 5. Grades mit 6 Koeffizienten: Wenn man von den 10 maximal möglichen Koeffizienten des 5. Grades die 4 „geradzahligen“ mit Null belegt, erhält man ein zweifach symmetrisches Kartennetz.
[Canters (2002), p. 227f., Tab. 5.23, Fig. 5.35 (b)]
Fifth-order transformation with one-fold symmetry
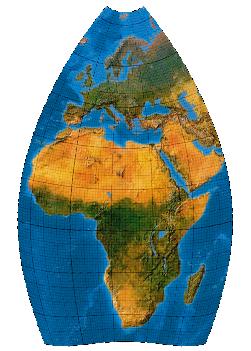
Polynome 5. Grades, eine Symmetrieachse. Interessant übrigens, wie es „die Polynome schaffen“, den Äquator (der ja eine sphärische Gerade ist) gerade abzubilden - solange er über Land verläuft. Meeresflächen hat Canters nicht mehr in seine Optimierung einbezogen.
[Canters (2002), p. 227f., Tab. 5.23, Fig. 5.36 (b)]
Fifth-order transformation without symmetry
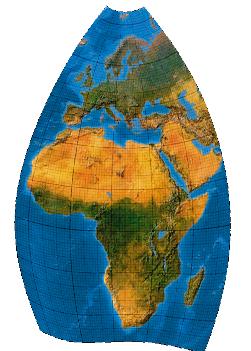
Wenn nun alle 10 Koeffizienten, die der 5. Grad zulässt, mit (Nicht-Nullen) belegt werden, wirds wieder zugleich unsymmetrisch und sehr verzerrungsarm. Dies ist das Netz, welches die Landflächen Europas und Afrikas mit den geringstmöglichen Winkelverzerrungen flächentreu abbildet.
[Canters (2002), p. 227f., Tab. 5.23, Fig. 5.37 (b)]
Die Eurafrica-Bilder dieser Seite haben den Maßstab 1:400.000.000 (bei 254 dpi).
Bei Rechnen mit Vimage ist zu beachten: Es handelt sich um Post-Projektionen, die nur die zweite Abbildung besorgen. Zuerst ist der schiefachsige flächentreue Azimutalentwurf Erdkugel auf Kartenebene zu rechnen.
Weil die Polynome auf dem Einheitskugelradius als Einheit aufbauen fragen die Post-Projektionsprogramme erneut eine Maßstaszahl ab (obwohl der Maßstab ja schon in der 1. Stufe gerechnet wurde). Diese muss bei beiden Transformationen identisch angegeben werden.
Hier die Programme:
1. Stufe
Schiefachsiger flächentreuer Azimutalentwurf (Programm)
Schiefachsiger flächentreuer Azimutalentwurf (Direktprogramm, Snyders Formel, etwas schneller)
2. Stufe (Post-Transformation)
Canters Low-error Projection (Eurafrica) P10 (Direktprogramm)
Canters Low-error Projection (Eurafrica) P11 (Direktprogramm)
Canters Low-error Projection (Eurafrica) P12 (Direktprogramm)
Canters Low-error Projection (Eurafrica) P13 (Direktprogramm)
Canters Low-error Projection (Eurafrica) P14 (Direktprogramm)
Canters Low-error Projection (Eurafrica) P15 (Direktprogramm)
Canters Low-error Projection (Eurafrica) P16 (Direktprogramm)
Canters Low-error Projection (Eurafrica) P17 (Direktprogramm)