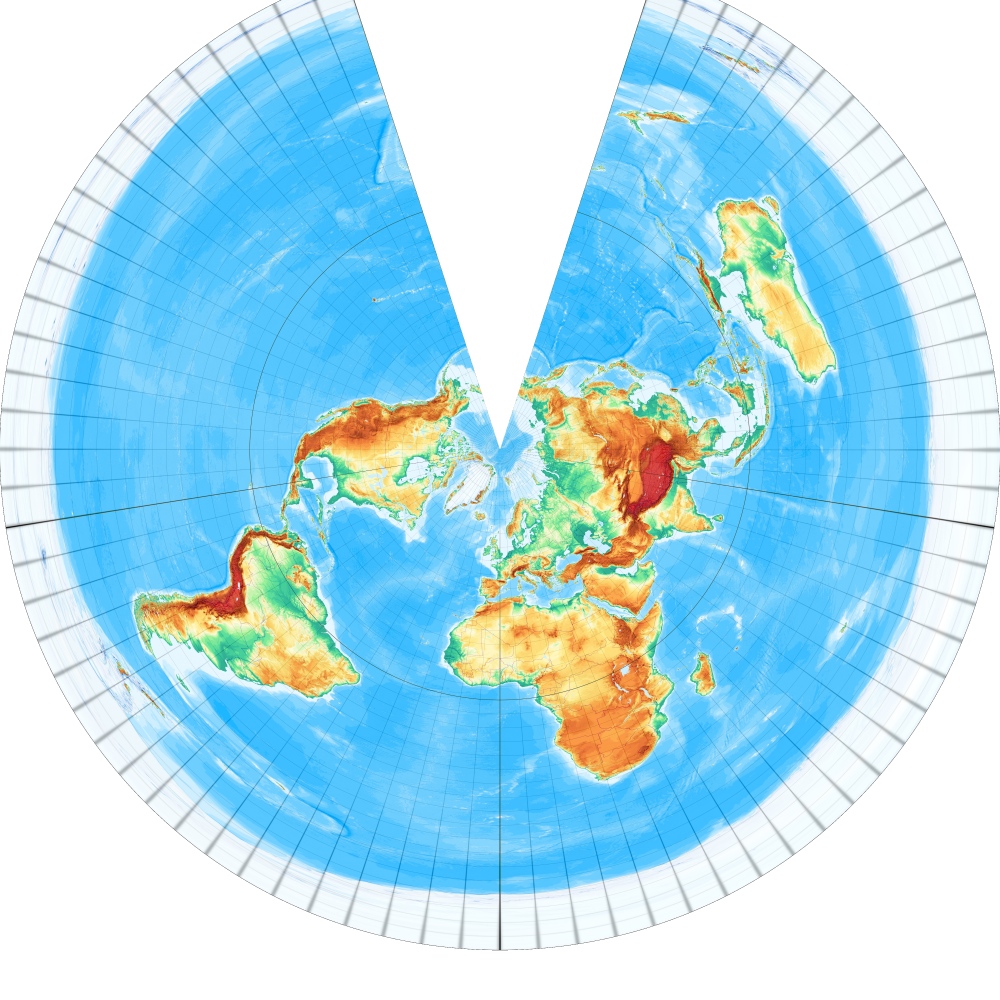
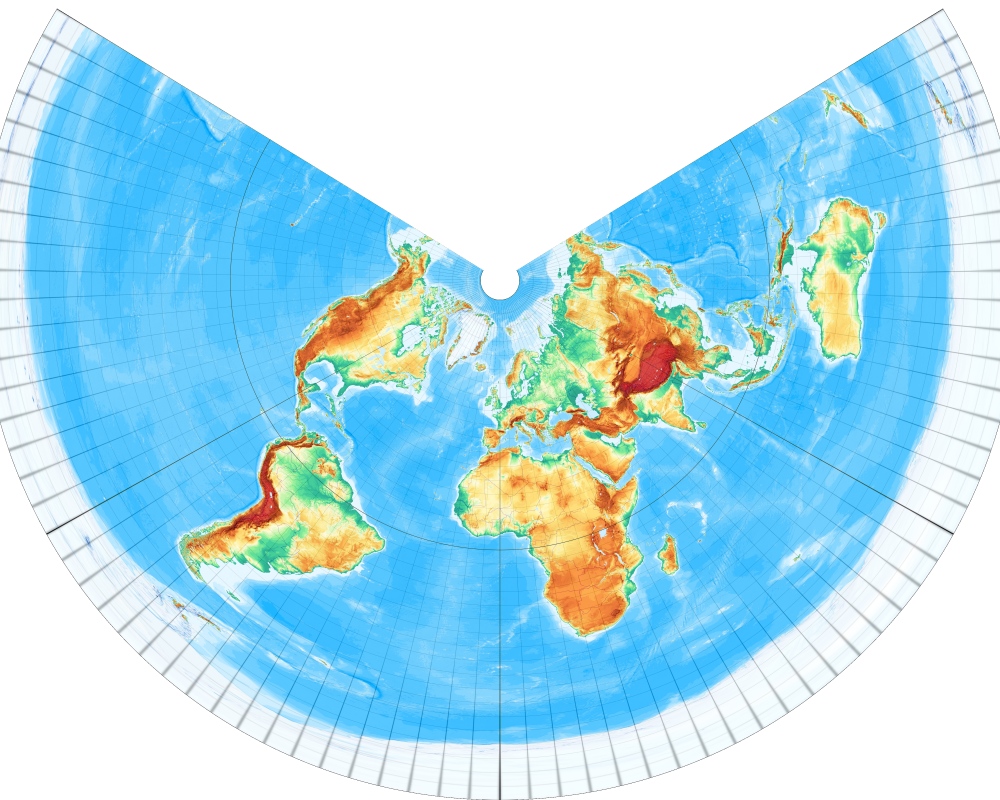
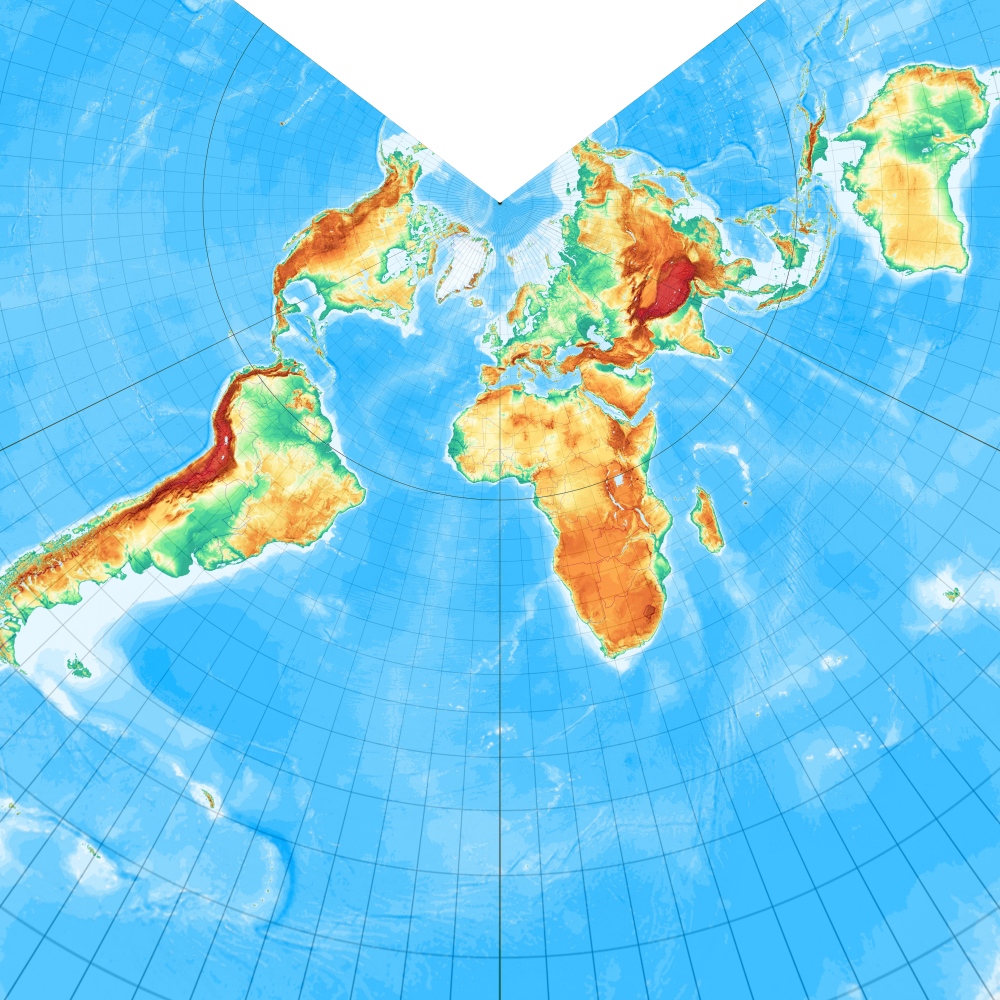
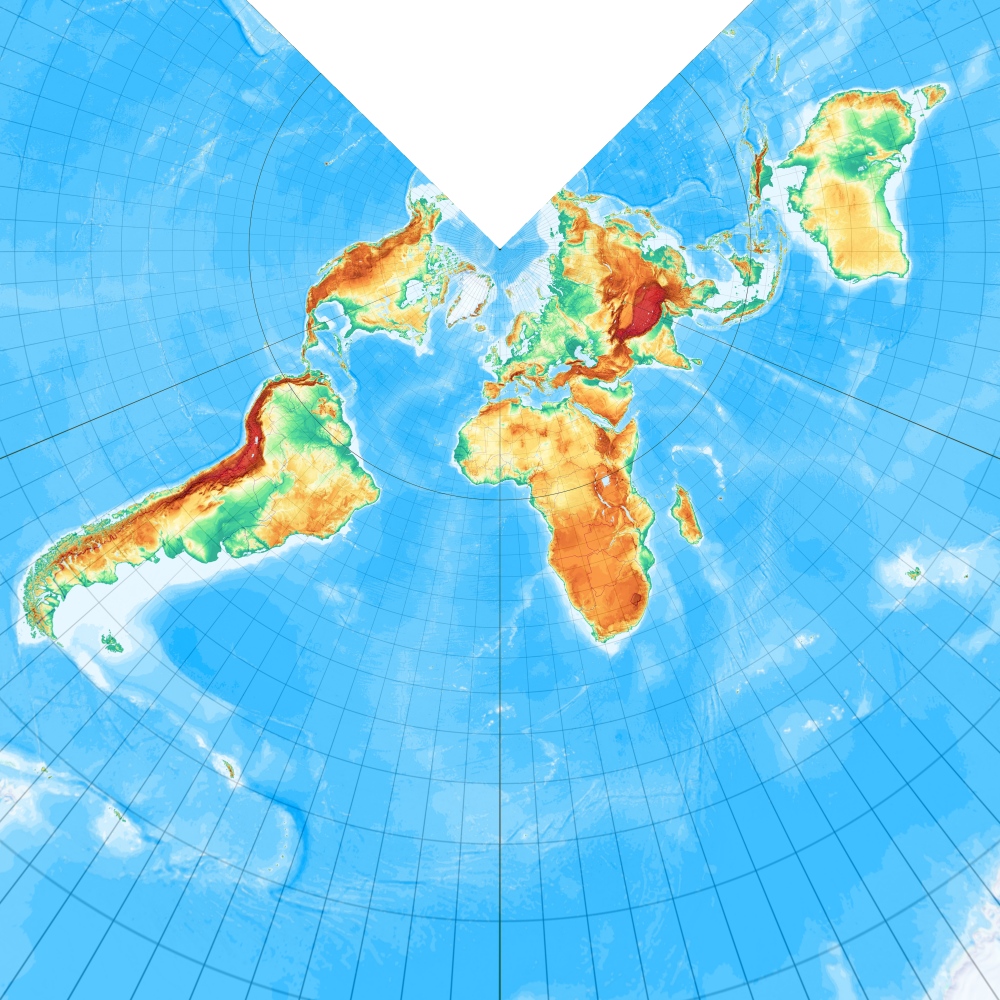
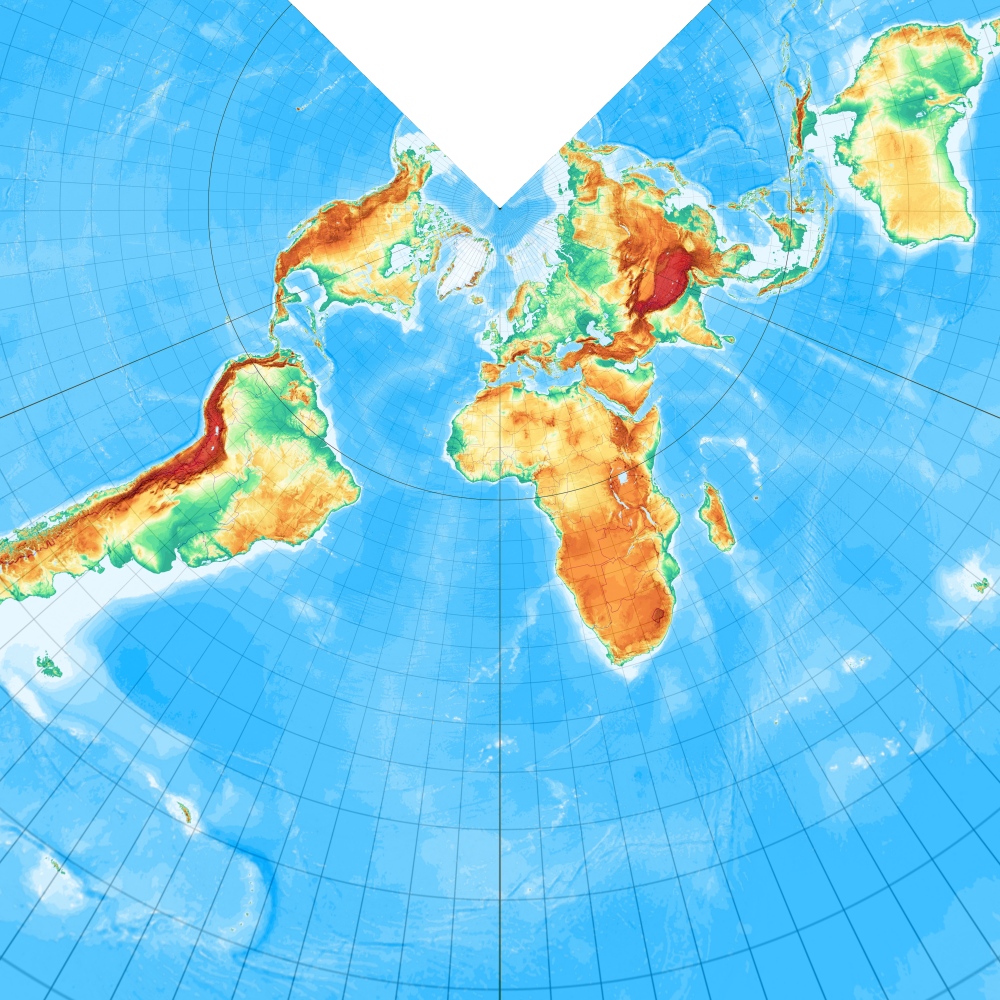
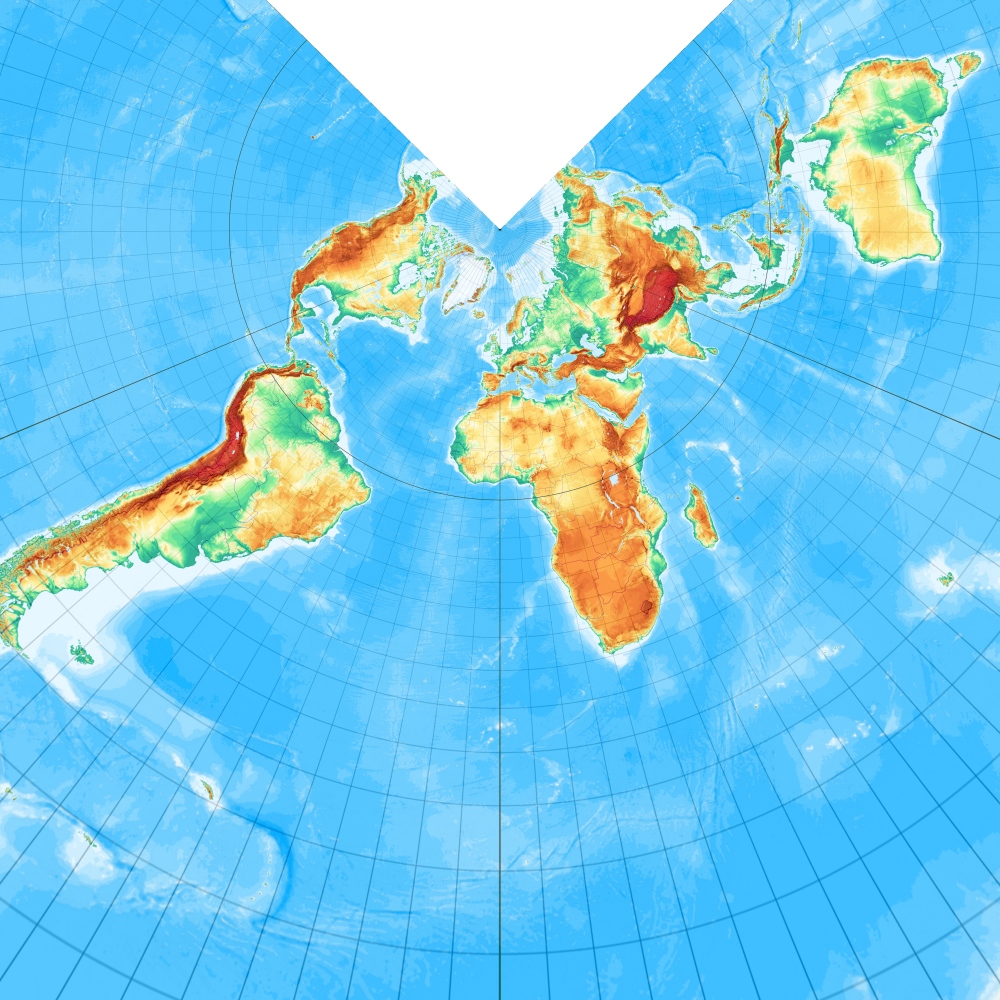
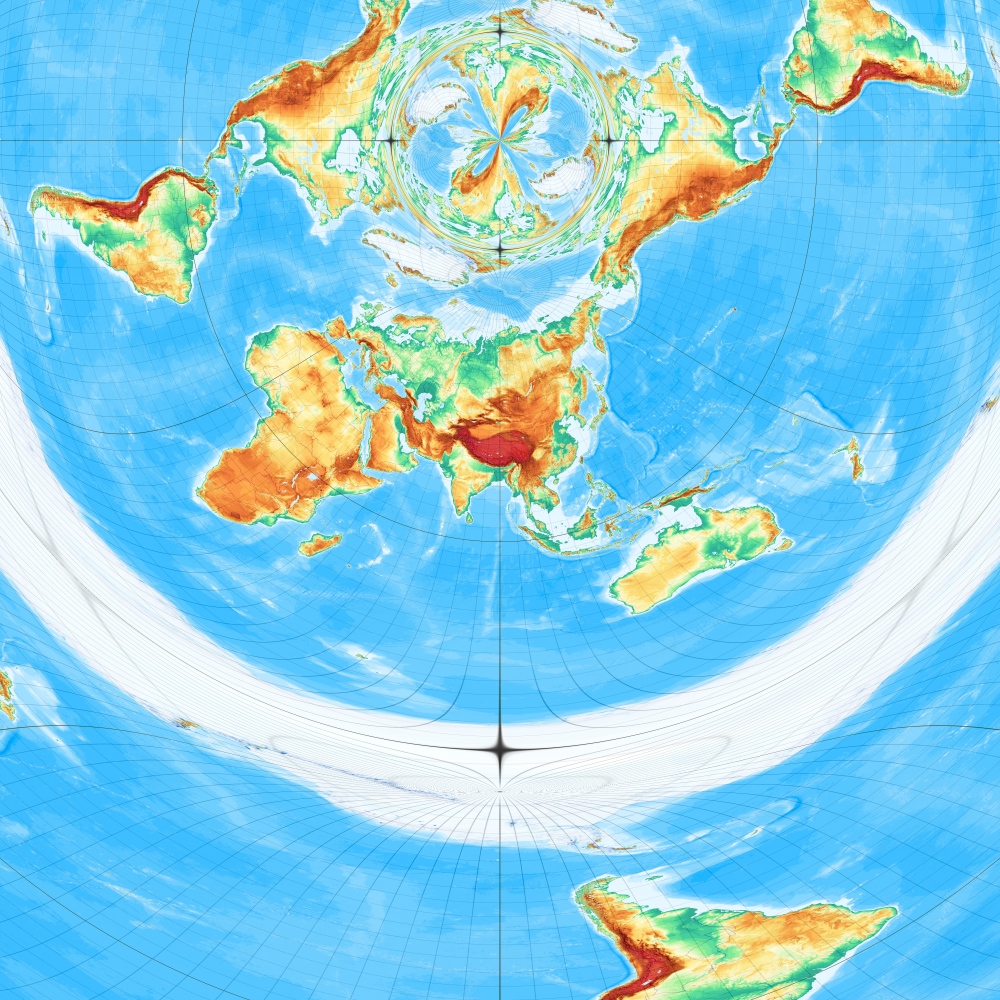
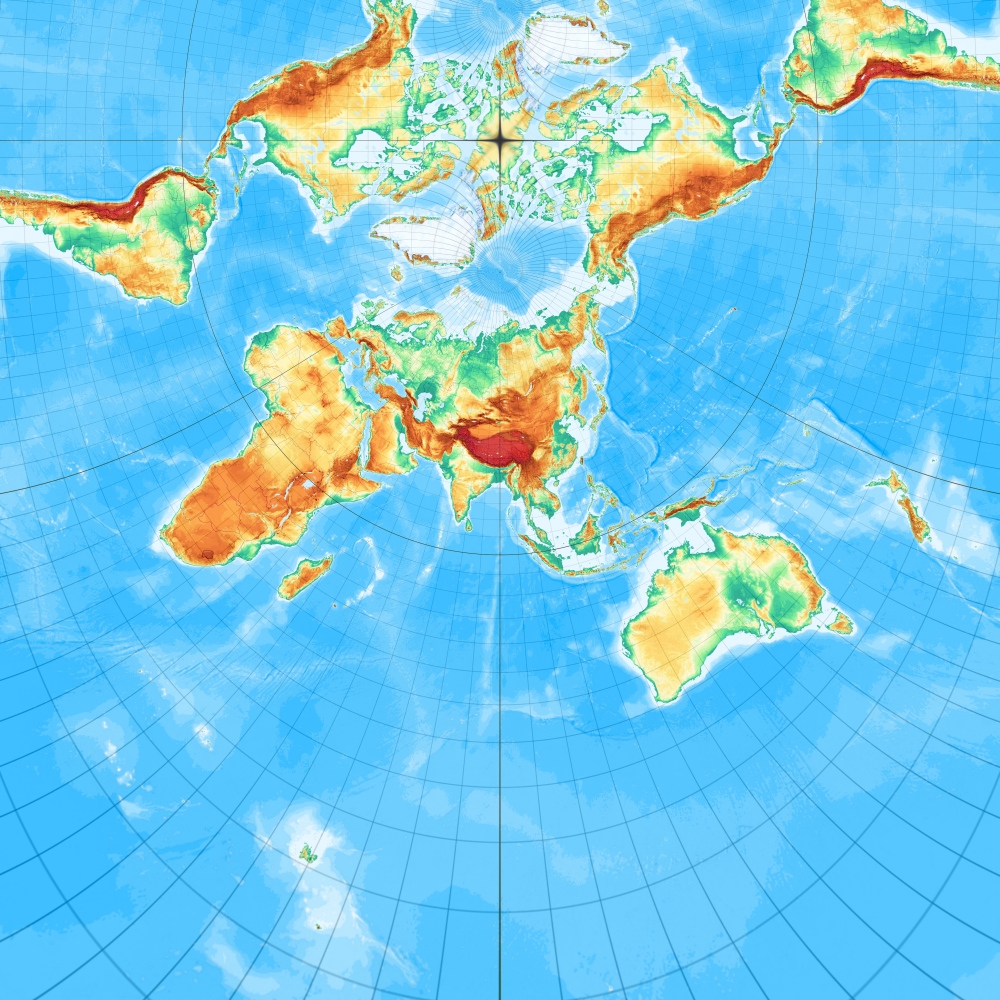
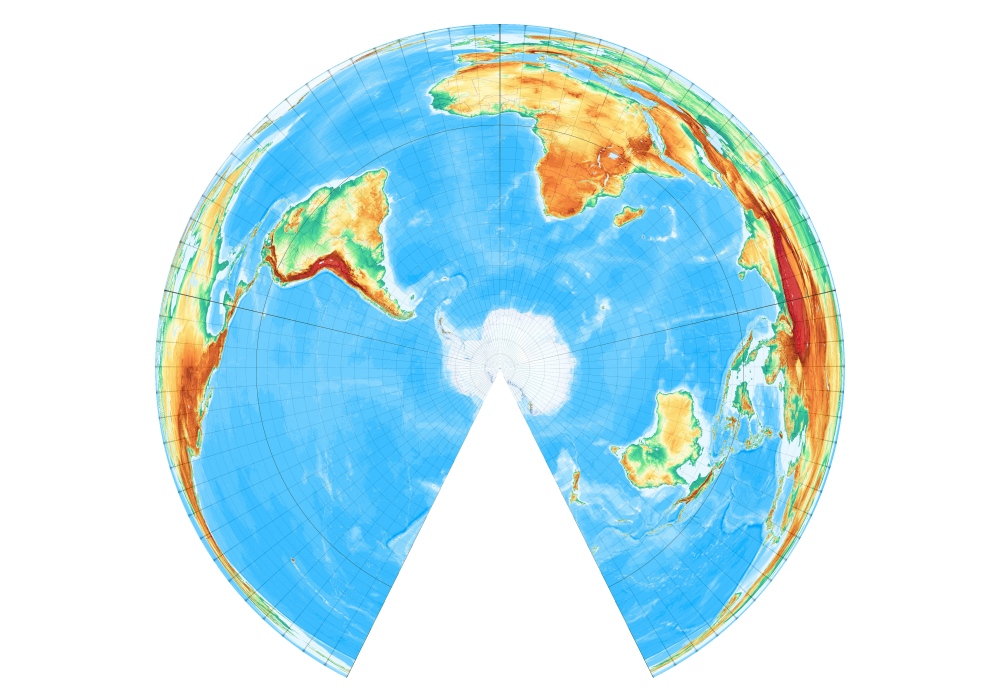
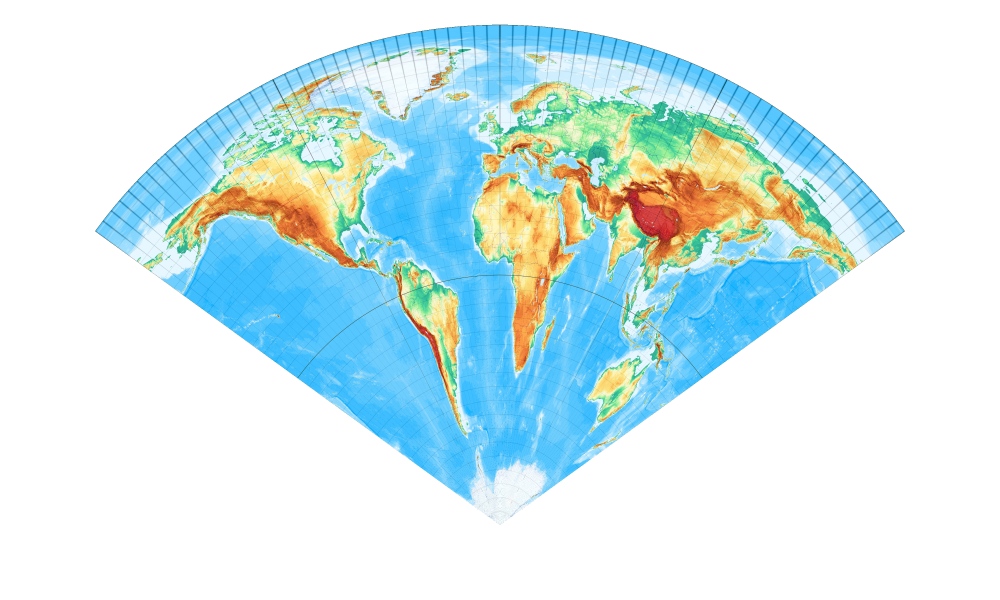
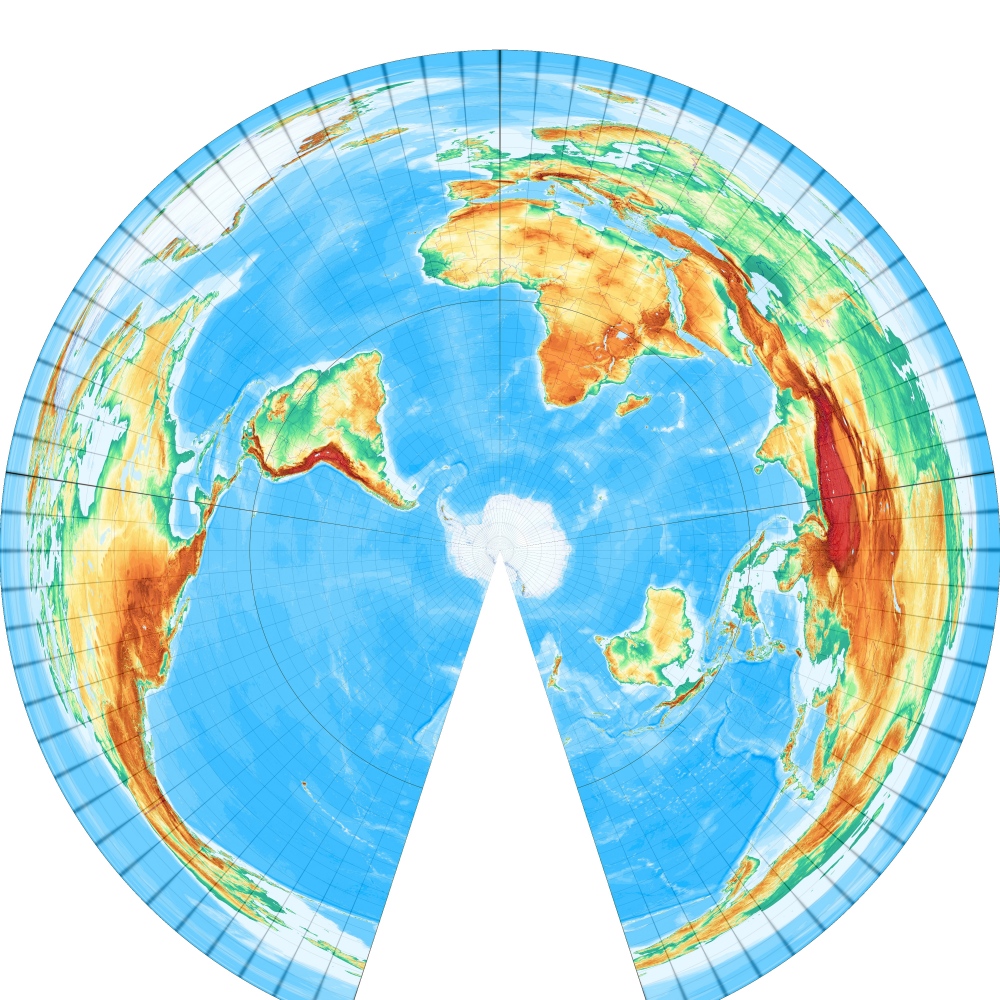
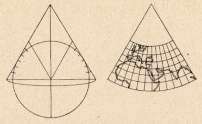
[Abbildung: Wagner, S. 33]

Kegelentwürfe sind eigentlich immer dann erste Wahl, wenn ein Gebiet zwischen einigen Dutzend und mehreren Tausend Kilometern Größe wiedergegeben werden soll, also Karten von Ländern bis Kontinenten.

Sie haben die Eigenschaft, dass die Meridiane gleichabständige Strahlen oder Strecken in Richtung Pol sind und die Parallelkreise Kreisbogenstücke, die die Meridianbilder rechtwinklig schneiden.

Der Winkel zwischen den Meridianen ist aber immer kleiner, als deren (geographische) Längendifferenz.

Indem man die Radien der Parallelkreise geeignet wählt, lässt sich ein Entwurf flächentreu, abstandstreu oder winkeltreu gestalten.

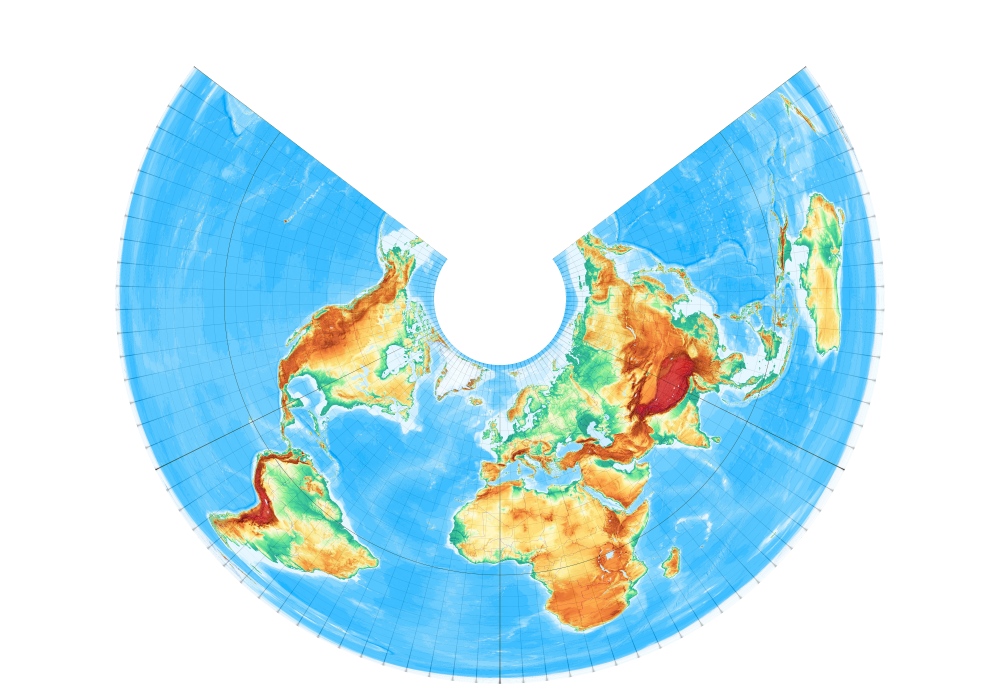
Die Forderung nach Flächentreue führt polwärts zu stark abnehmenden Parallelkreisabständen. Hier ein flächentreuer Entwurf auf einen Kegel mit einer Berührungsbreite von 45° Nord. [Entwurf 3 nach Wagner]. – Equal-area Conic with one standard parallel or Lambert Equal-area Conic (1772):

Der Entwurf lässt sich nach Lambert (1772) auch so gestalten, dass der Pol zum Punkt wird [Entwurf 3a nach Wagner]. – Equal-area Conic with one standard parallel, pole as point:

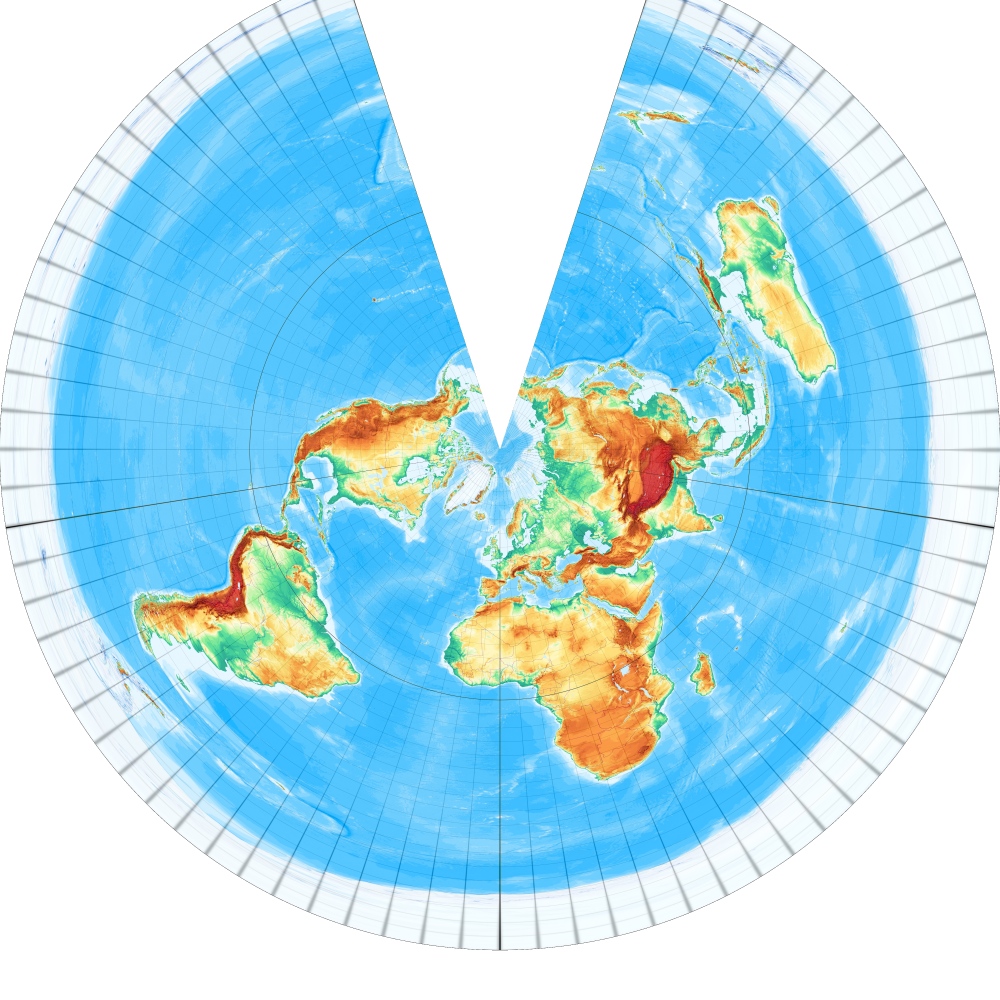
Häufig ist auch der Alberssche flächentreue Kegelentwurf aus dem Jahr 1805 anzutreffen, der zwei Parallelkreise (hier 15° und 75°) längentreu abbildet [Entwurf 4]. – Equal-area Conic with two standard parallels or Albers Equal-area Conic (1805):

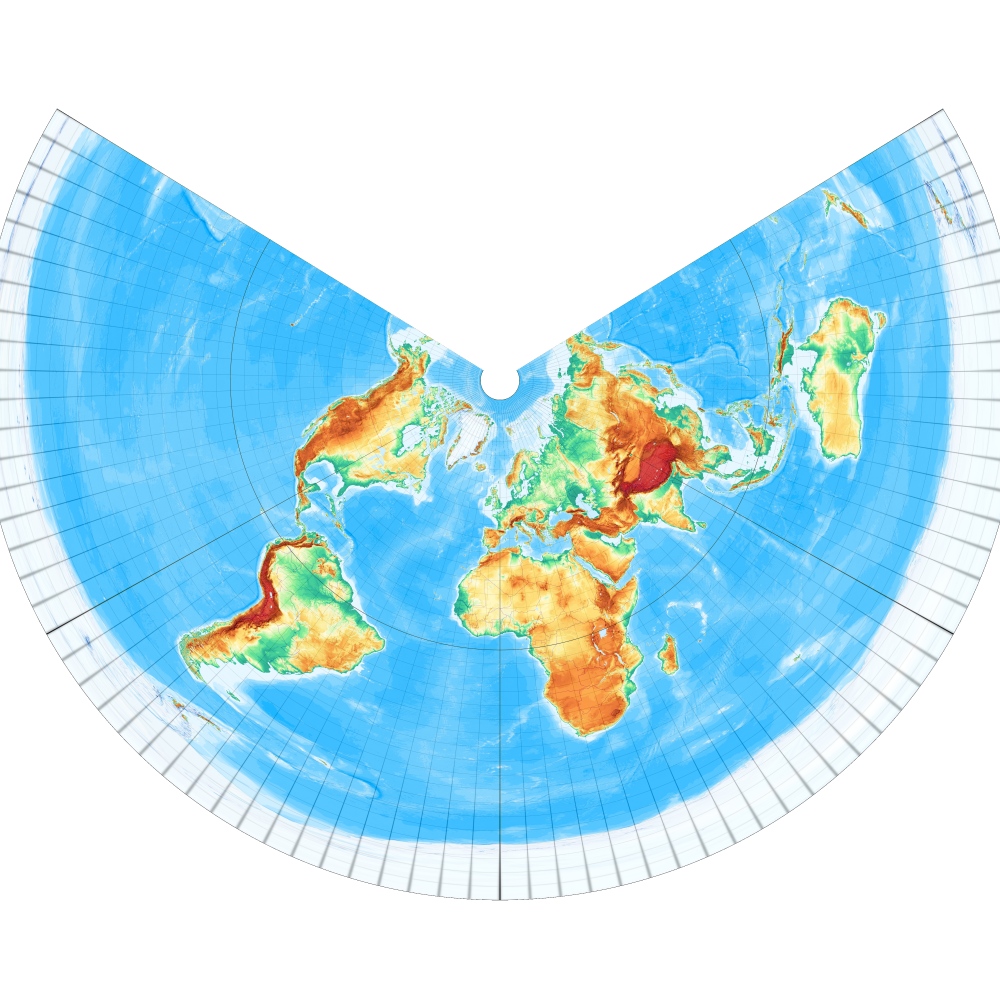
Das einfache Prinzip, alle Parallelkreise einfach in gleichem Abstand anzuordnen, führt zum abstandstreuen Kegelentwurf. Hier ein Berührungskegel mit einer Berührungsbreite von 45° Nord. Der Entwurf ist schon sehr alt und wird Ptolemäus zugeschrieben [Entwurf 1 nach Wagner]. – Equidistant Conic with one standard parallel:

Der Entwurf lässt sich auch so ausführen, dass der Pol zu einem Punkt wird, was allerdings kaum genutzt wird. [Entwurf 1a nach Wagner]. – Equidistant Conic with one standard parallel, pole as point:

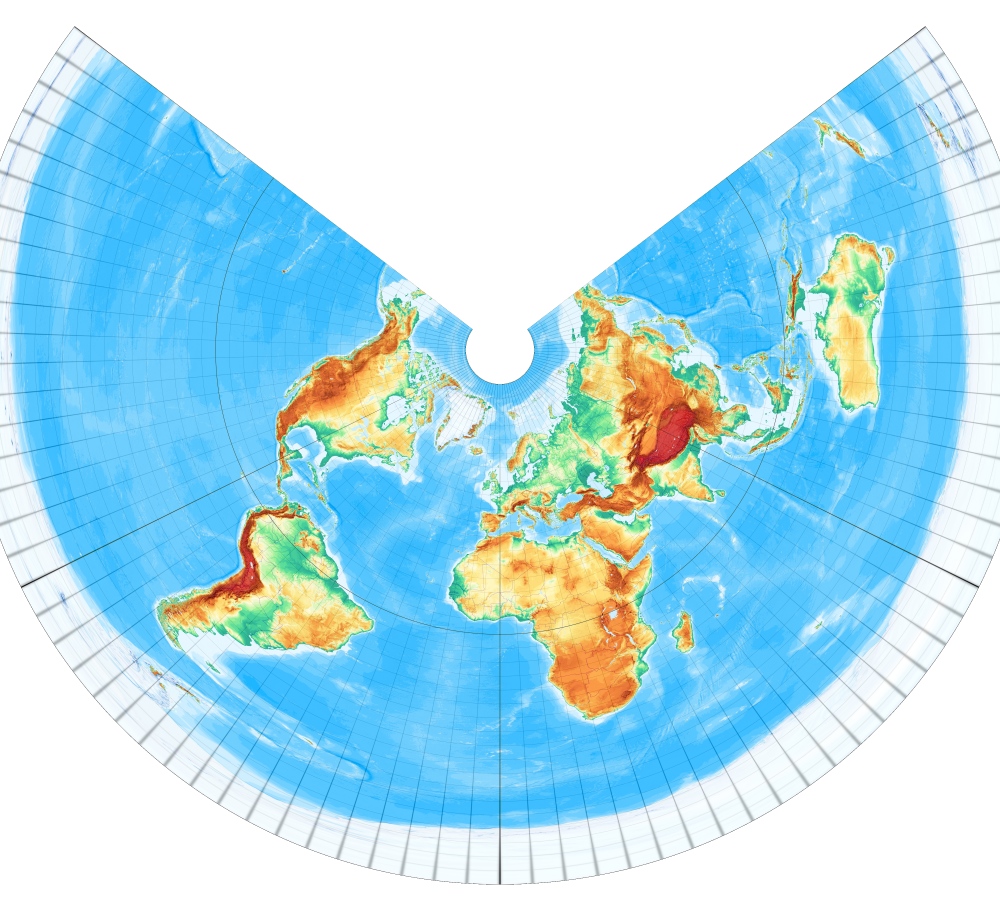
Gebräuchlicher ist eine Variante mit 2 längentreuen Parallelkreisen, die auf de l'Isle 1745 zurückgeht. Hier mit 15° und 75° [Entwurf 2 nach Wagner] – Equidistant Conic with two standard parallels or De L'Isle Conic (1745):

Zum Schluss lassen wir einmal Bruder Winkeltreue gewinnen. Auch hier wieder ein Netz mit einer Berührungsbreite von 45° nördlicher Breite. Wie oft bei winkeltreuen Entwürfen wird die Abbildung unbegrenzt groß: Der Südpol hat den Radius unendlich. Dieser Entwurf stammt ebenfalls von Lambert (1772). Beim winkeltreuen Kegelentwurf ist der Pol immer automatisch ein Punkt. [Entwurf 5 nach Wagner]. – Conformal Conic with one standard parallel:

Der Entwurf lässt sich auch mit zwei (gegebenen) längentreuen Parallelkreisen als winkeltreuer Schnittkegelentwurf [I] ausführen. Es ergibt sich dann aber kein neues Netzbild, sondern lediglich eine gewisse Verkleinerung (Wagner S. 65). – Conformal Conic with two standard parallels:

Winkeltreuer [Schnitt-]Kegel II (nach Wagner): Bei aufmerksamer Lektüre des Wagner bemerkt man noch zwei Untervarianten, zunächst die sog. günstigste Abbildung einer Kegelzone. Dies ist eigentlich ein Berührungskegel, allerdings wird der Berührungsparallel anhand von zwei Parallelkreisen so bestimmt, dass die Verzerrungen in jenen gleich sind. Infolgedessen erscheint er dem Anwender als Schnittkegel (Wagner S. 64). – Conformal Conic, best mapping between two parallels:

Winkeltreuer Schnittkegel III (nach Wagner): Schließlich kann ein Schnittkegel so gelegt werden, dass die Verzerrungen an zwei Grenzparallelen und einem Mittelparallel gleich sind. Hierbei sind allerdings die errechneten Schnittparallelen nicht mit den gegebenen Grenzparallelen identisch. Sog. winkeltreuer Kegelentwurf mit gleichstarken Verzerrungen in Mittel- und Grenzparallel. Das ist das gerechnete Beispiel im Wagner S. 66-68. – Conformal Conic, equal [minimal] distortion in two outer parallels and a central parallel:

Die Netzbilder aller vier winkeltreuer Kegel sind weitgehend identisch.

Im Gegensatz zu Zylindern und Ebenen wurden Kegel bisher kaum schiefachsig an unserer Mutter Erde angeordnet. Das lag im Analogzeitalter natürlich am Rechenaufwand. - Warum aber eigentlich nicht? Mit schiefen (obliquen) Kegeln lassen sich langgestreckte Erdoberflächenausschnitte sehr gut abbilden, insbesondere, wenn die Achse des Gebietes gekrümmt ist.

Folgerichtig hat Prof. Frank Canters aus Brüssel 2002 schiefe Kegel zur Abbildung von Amerika vorgeschlagen. Siehe hierzu Canters Netze IV

Hier ein schiefer Kegel, dessen Achse in 75°N, 90°W die Erde durchsticht. Das eigenartige Nordmeer ist folglich die Hudson-Bay, in der dieser Punkt liegt. Schnittkegel mit Schnittparallelen 29° und 31°.

Flächentreuer Kegelentwurf in schiefer Lage. – Oblique Equal-areal Conic:

Abstandstreuer Kegelentwurf in schiefer Lage. – Oblique Equidistant Conic:

Winkeltreuer Kegelentwurf in schiefer Lage. – Oblique Conformal Conic:

Der Kegel wird mehrfach umlaufend abgewickelt; das ergibt die mehrfachen Amerikabilder.

Sieht doch interessant aus, oder? Wenn das der olle Lambert wüßte.

Wenn man die gewöhnlichen „Pol-als-Punkt-Kegel“ mit einem Südparallel durchrechnet, wird das schief gehen, denn dann rechnet er 45° Süd und – Nordpol. Also braucht man eine zweites Programm mit dem Südpol als Punkt.

Flächentreuer Kegelentwurf mit Südpol als Punkt, 45° längentreu. Equal-area cone with standard parallel 45°:

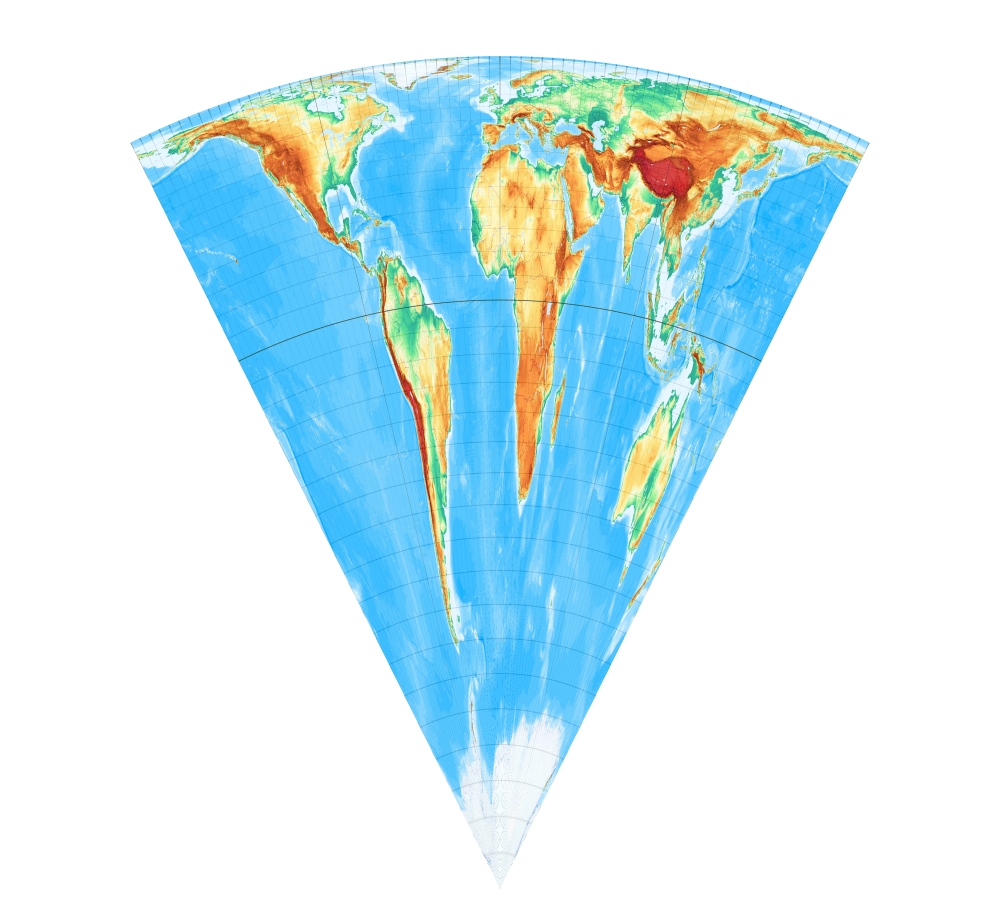Das wird meist genau falschherum sein, also ...

Flächentreuer Kegelentwurf mit Südpol als Punkt, -45° längentreu. Equal-area cone with standard parallel -45°:

So ist es wohl eher richtig.

Abstandstreuer Kegelentwurf mit Südpol als Punkt, 45° längentreu. Equidistant cone with standard parallel 45°:

Falsch herum.

Abstandstreuer Kegelentwurf mit Südpol als Punkt, -45° längentreu. Equidistant cone with standard parallel -45°:

Wohl eher richtig.

Assemblerprogramme:

Bei den Kegelentwürfen ist der Rechenmittelpunkt (der Pol) nicht zugleich Kartenmittelpunkt, sondern gewöhnlich nach oben versetzt. Daher gibt es zwei Programmreihen. Selbstzentrierende Programme versetzen den Pol so, dass der Mittelpunkt des gegebenen Erdoberflächenstückes Kartenmittelpunkt wird. Bei den polversetzenden Programmen wird ein Polversatz abgefragt.

Selbstzentrierende Programme in polständiger Lage

Flächentreuer Kegelentwurf
Flächentreuer Kegelentwurf mit dem Pol als Punkt (Lambert)
Flächentreuer Kegelentwurf mit zwei längentreuen Parallelkreisen (Albers)
Abstandstreuer Kegelentwurf
Abstandstreuer Kegelentwurf mit zwei längentreuen Parallelkreisen
Abstandstreuer Kegelentwurf mit dem Pol als Punkt
Winkeltreuer Kegelentwurf
Winkeltreuer Schnittkegelentwurf (I) mit zwei gegebenen längentreuen Parallelkreisen
Winkeltreuer Kegelentwurf II, günstigste Abbildung einer Kegelzone
Winkeltreuer Schnittkegelentwurf III, gleichstarke Verzerrung in Mittel- und Grenzparallel

Polversetzende Programme in polständiger Lage

Flächentreuer Kegelentwurf
Flächentreuer Kegelentwurf mit dem Nordpol als Punkt (Lambert)
Flächentreuer Kegelentwurf mit dem Südpol als Punkt (Lambert)
Flächentreuer Kegelentwurf mit zwei längentreuen Parallelkreisen (Albers)
Abstandstreuer Kegelentwurf
Abstandstreuer Kegelentwurf mit zwei längentreuen Parallelkreisen
Abstandstreuer Kegelentwurf mit dem Nordpol als Punkt
Abstandstreuer Kegelentwurf mit dem Südpol als Punkt
Winkeltreuer Kegelentwurf
Winkeltreuer Schnittkegelentwurf (I) mit zwei gegebenen längentreuen Parallelkreisen
Winkeltreuer Kegelentwurf II, günstigste Abbildung einer Kegelzone
Winkeltreuer Schnittkegelentwurf Wagner III, gleichstarke Verzerrung in Mittel- und Grenzparallel

Schiefachsige Kegel (immer Schnittkegel, immer selbstzentrierend)

Flächentreuer Schnittkegelentwurf (Albers)
Abstandstreuer Schnittkegelentwurf (De L'Isle)
Winkeltreuer Schnittkegelentwurf

08.10.2014 Durchsicht
17.03.2021 W100