... da könnte man meinen, dass die allerbeste Projektion längst gefunden worden ist und es nichts Neues mehr zu entdecken gibt.
Das stimmt nicht ganz. In den Kartographischen Nachrichten 6/2004 publizierten die ungarischen Kartographen Janós Györffy und István Klinghammer einige neue Projektionen, mit denen sich Europa noch mit etwa 10 bis 20 % geringeren Verzerrungen abbilden lässt, als mit den sonst üblichen Kartennetzen.
Die Netze wurden so optimiert, dass Europa zwischen 10° West und 60° Ost, 35° und 70° nördlicher Breite mit minimalen Verzerrungen wiedergegeben wird.
In dem Aufsatz schlägt Györffy zunächst einen orthogonalen pseudopolykonischen Optimalentwurf mit 5 Koeffizienten vor. Hier der Entwurf für die ganze Welt ...
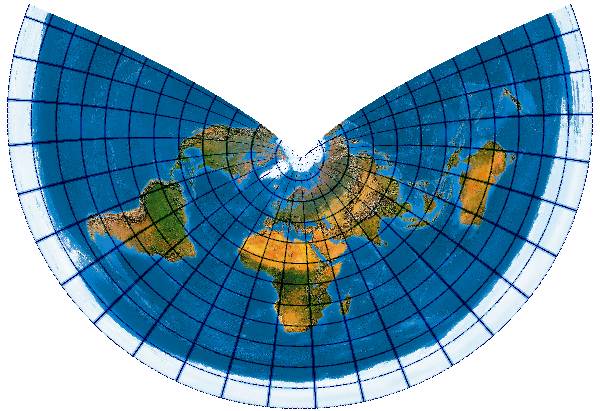
... und für Europa:
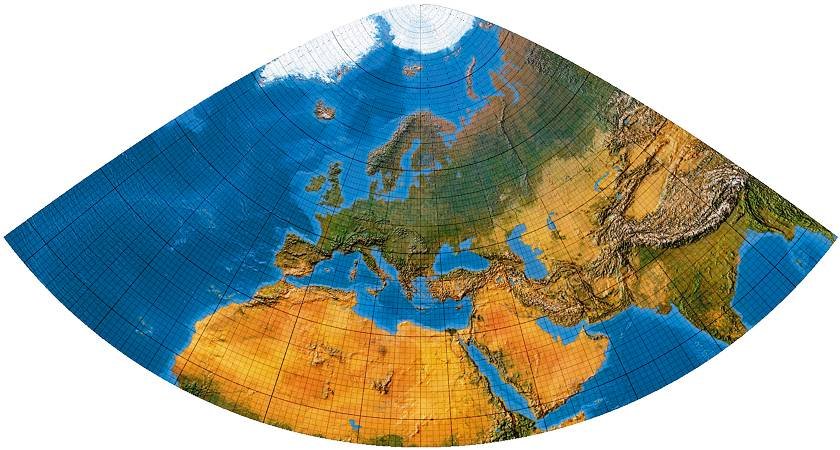
Orthogonal heisst, dass sich Meridiane und Parallelkreise rechtwinklig schneiden. Wenn man auf diese Forderung verzichtet, so können die Verzerrungen noch ein wenig weiter gemindert werden ...
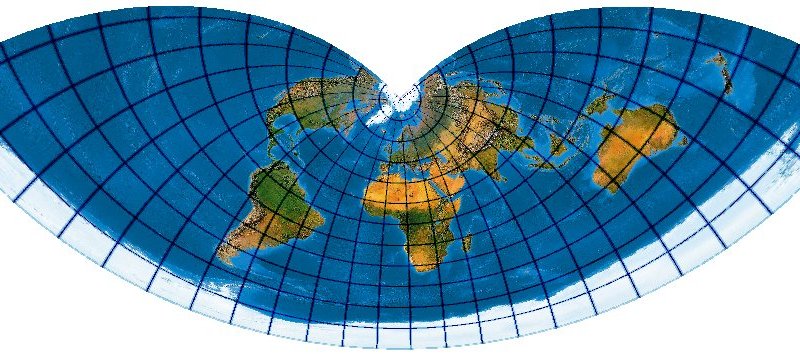
... und man gelangt zum allgemeinen pseudopolykonischen Optimalentwurf mit 8 Koeffizienten. Polykonisch heisst, dass die Parallelkreise als konzentrische Kreise abgebildet werden. Es entsteht das Bild, das unsere Welt in einem eleganten vollkommenem Kreisrahmen abbildet:
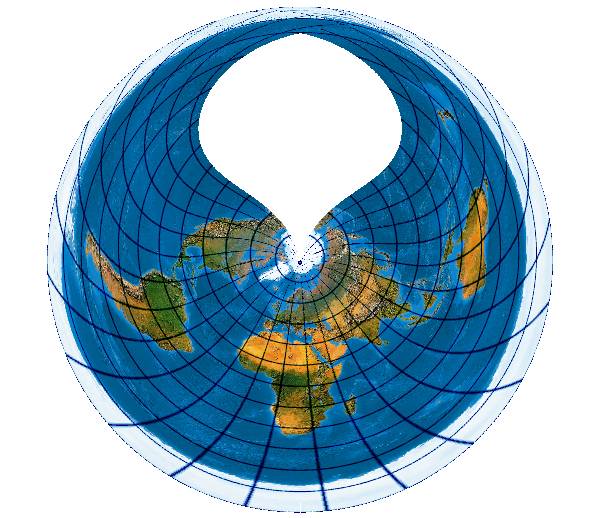
Europa wird mit nur ganz geringen Verzerrungen wiedergegeben:
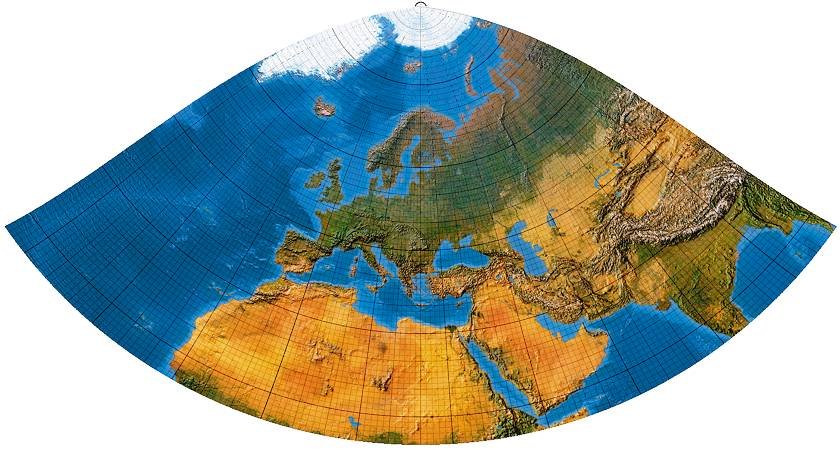
Die geschwungenen Aussenmeridiane verdanken ihre Form kubischen Polynomen.
Es geht aber noch etwas raffinierter. Die Idealabbildung verwendet nicht weniger als 17 Koeffizienten und hat die allergeringsten Verzerrungen. Die Koordinaten durchlaufen komplizierte Kurven dritten Grades mit Maxima und Wendepunkten. Hier das Resultat einer Berechnung:
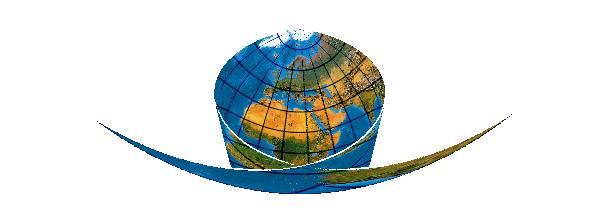
Die Generierung der Weltkarte musste hinter dem Ural und auf Grönland abgebrochen werden, weil die kubischen Polynome Südamerika und Indonesien diesselben Kartenkoordinaten zuweisen wie Europa. Eine Abbildung der gesamten Erdoberfläche ist nicht mehr möglich.
Rechnet man aber nur europäisches Gebiet, so erhält man eine ausgezeichnete Kartengeometrie:
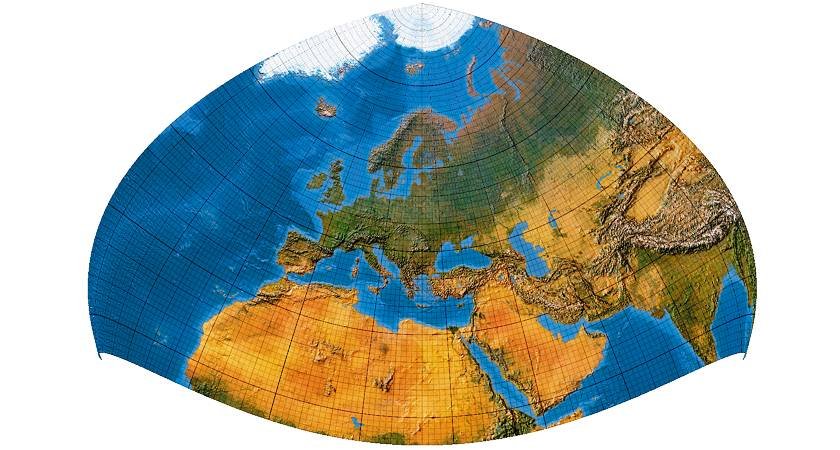
An den Südecken des Bildes ist gerade zu erkennen, wie ein Parallelkreis „rückläufig“ wird. Wir erhalten ein Netz, welches mit seinen geschwungenen Meridianen und Parallelkreisen geringste Verzerrungen mit einem ästhetischen Netzbild vereinigt.
Hier Györffys orthogonaler pseudopolykonischer Optimalentwurf für Europa im Großformat (Maßstab 1:200 Millionen bei 254 dpi Auflösung):
Auf http://lazarus.elte.hu/hun/digkonyv/sc/sc12/01gyj.pdf gibt es einen weiteren Aufsatz von Janos Györffy, in dem er orthogonale (also Netze mit sich rechtwinklig scheidenden Gitternetzlinien) pseudopolykonische Kartennetze vorstellt.
Von den im Aufsatz genannten 20 Entwürfen, die Györffy gerechnet hat, werden 6 formelmäßig vorgestellt. Hier die beiden Netze mit den geringsten ermittelten Verzerrungen.
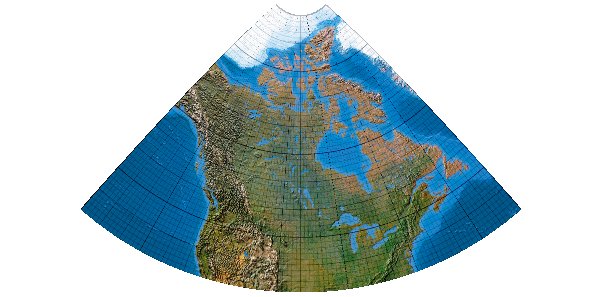
Als „P1“ habe ich das Netz mit dem Eak-Wert vom 0,00637 bezeichnet. Das Netz hat minimierte Verzerrungen im Gebiet von 45° bis 75° N und 140° bis 60° W und stellt folglich eine Optimierung für Kanada dar. Mittelmeridian ist 100° W.
Die gesamte Erde in Standardmaßstab 1:800 Millionen:

Ausschnitt Kanada 1:200 Millionen:
Der „P2“ ist der Entwurf mit Eak=0,00442, der das Gebiet von 35° bis 70° N und 10° W bis 30° E - also das Gebiet der Europäischen Union - optimiert. Dabei wird der Mittelmeridian auf 10° E gelegt.
Györffy P2, gesamte Erde im Standardmaßstab 1:800 Millionen:
Györffy P2, Europäische Union 1:200 Millionen:

Im Gegensatz zu den Hammondschen Netzen (mit denen z. B. die Kontinentkarten von Meyers Großem Weltatlas entworfen wurden) haben Györffys Entwürfe den Vorteil, dass die Formeln bekannt sind und sich folglich nachprogrammieren lassen.
Hier die Assemblerprogramme der Netze:
Györffys orthogonaler pseudopolykonischer Optimalentwurf für Europa (E1) (Direkttransformationprogramm)
Györffys allgemeiner pseudopolykonischer Optimalentwurf für Europa (E2) (Direkttransformationprogramm)
Györffys Idealabbildung für Europa (E3) (Direkttransformationprogramm)
Györffys orthogonaler pseudopolykonischer Entwurf für Kanada (P1) (Direkttransformationprogramm)
Györffys orthogonaler pseudopolykonischer Entwurf für die Europäische Union (P2) (Direkttransformationprogramm)
Ich bedanke mich herzlich bei Janós Györffy, der mir die Formeln der Entwürfe E2 und E3 zugesendet hat.
12.02.2007: Erneuter Dank an Janos Györffy, für den Hinweis auf den Aufsatz mit dem P1 und dem P2.