Pseudozylindriche Projektionen sine unechte Zylinderprojektionen, bei denen die Meridiane auch gekrümmte (und geknickte) Formen annehmen können. Die Parallelkreise sind aber gerade Linien.
„Pseudocylindricals“ eignen sich insbesondere für Abbildungen der gesamten Erdoberfläche. Es gibt eine große Vielfalt von Varianten, die sich allerdings teilweise nur ganz geringfügig unterscheiden. Gerald I. Evenden führt in seiner Comprehensive Library 2004, 2005, 2008 insgesamt 46 Vertreter auf.
Wichtige Pseudozylinder sind das Netz des Apianus, der Mercator-Sanson-Entwurf, der Mollweidesche Entwurf, die Wagnerschen Entwürfe I bis VI und die Robinson-Projektion.
Siehe diese auf den Seiten Von Apian bis Winkel und Wagners Weltkartennetze.
Canters Pseudozylinder sind nur eine ganz kleine Untermenge der Entwicklungen von Prof. Canters und stehen auf einer Extra-Seite, die ausschließlich Canters-Projektionen zeigt.
Max Eckert, mit seinem zweibändigem Werk „Die Kartenwissenschaft“ einer der Begründer der modernen wissenschaftlichen Kartographie, hat 6 Kartennetzentwürfe entworfen und veröffentlicht. Hier einmal sämtliche Eckert-Entwürfe, auch die selten zitierten Entwürfe I und II mit den ungewöhnlichen Meridianen in Trapezform und dem späteren „Eckert-Greiffendorf“:
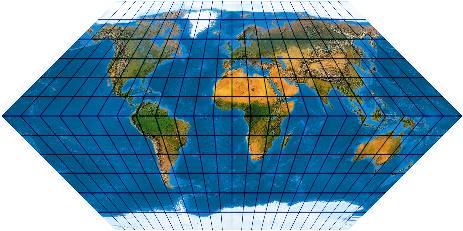
Hier die Karte als Großformat (ca. 800 kByte) im Maßstab 1:200.000.000 (bei 254 dpi).
[Evenden: 6.2.21]
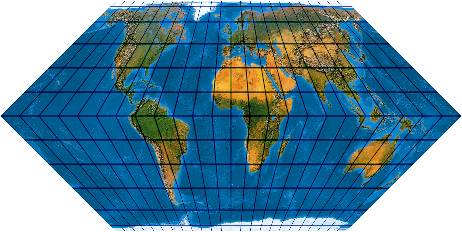
[Evenden: 6.2.22]
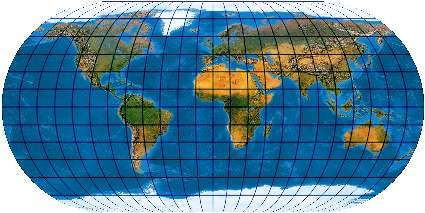
[Wagner: 23a, Evenden: 6.2.13]
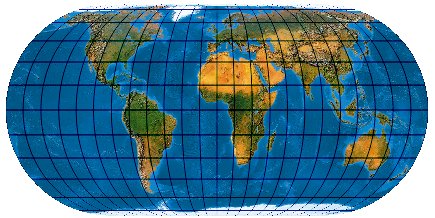
[Wagner: 23b, Evenden: 6.2.10]
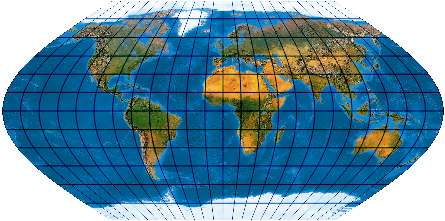
[Wagner: 22a, Evenden: 6.2.3]
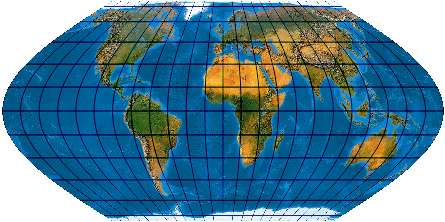
[Wagner: 22b, Evenden 6.2.1 (2.)]
Den „Eckert-Greiffendorf“ hat Max Eckert 1935 entwickelt. Zur Unterscheidung des Entwurfs von seinen 6 früheren Entwicklungen trifft es sich ganz gut, dass Eckert in seinen späteren Lebensjahren den Namenszusatz „Greiffendorf“ angenommen hatte.
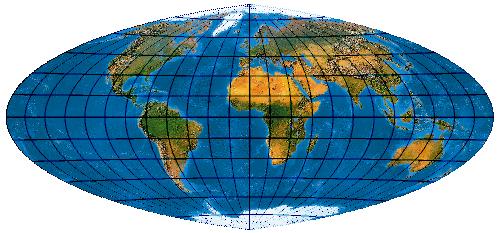
(Anmerkung: Das Netz hat ganz leicht durchgebogene Parallelkeise und gehört deswegen genau genommen gar nicht hier auf die Pseudozylinder-Seite.)
Das Grab Max Eckert-Greiffendorfs befindet sich übrigens auf dem evangelischen Friedhof in Löbau.
Den Eckert IV konstituiert eine transzendente Gleichung, deren Nullstellen nur iterativ gefunden werden können. Hier schlägt Wagner 2 Alternativformeln vor, die algebraisch auflösbar sind.
Wagner hat diesen Schöpfungen keinen Namen gegeben, weshalb wir sie behelfsweise als Y1 und Y2 eingliedern. Ein seltener und schöner Jagderfolg.
Der Wagner Y1 versucht den Eckert möglichst authentisch zu adaptieren.
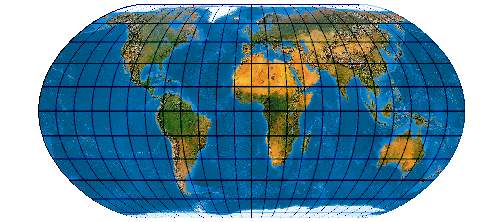
[Wagner 1949 S. 222 oben]
Der Wagner Y2 hingegen gestattet es, zwei Parallelkreise längentreu abzubilden. Hier ein Beispiel mit längentreuen 45°-Parallelkreisen:
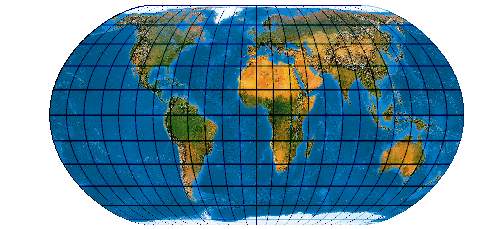
[Wagner 1949 S. 222 oben]
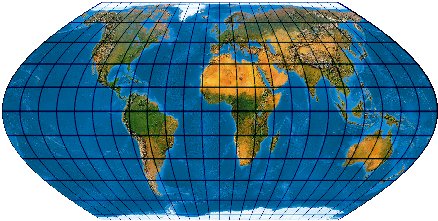
Ein Grund, warum sich der Eckert VI nie so richtig durchsetzen konnte, war die recht „spitze“ Sinuskurven-Außenform. 1992 veröffentlichte Carlos A. Furuti eine Eckert-VI-Weiterentwicklung, bei der die Meridiane keine vollen (180°-)Sinuskurven sind, sondern lediglich (auf 57,29577951°/90°) reduzierte Sinusbogenstücke. Das führt zu einer gefälligeren Außenform. (Furuti: Uma Projeção Cartográfica Equivalente.)
The Eckert meridian curves are full (180°) sine curves and near the equator very „sharp“.
The Eckert-Furuti meridian images doesn't have a (full) half sine phase, he reduces it on 57,29°/90° and the result is a
better earth outline shape. Here its (non publicated) inversion:
(2) phi = arcsin ( sin t / s1 )
(3) lambda = x / z * cos t
with the constants s1 = sin 1; T = R / root(pi/2*s1); z = 2 / pi. x, y, phi, lambda
are the co-ordinates.
 The difference between the Eckert VII and the Furuti-Eckert.
The difference between the Eckert VII and the Furuti-Eckert.
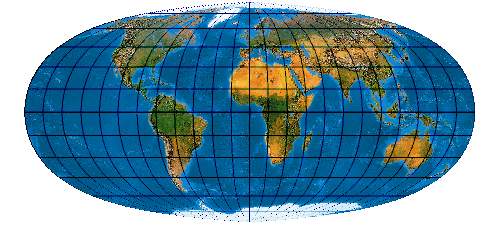
[Evenden 2004: 6.2.24]
(Identisch mit dem Wagner I)
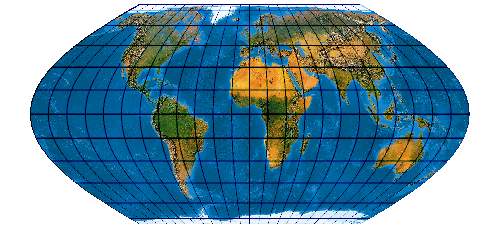
[Evenden 2004: 6.2.4)]
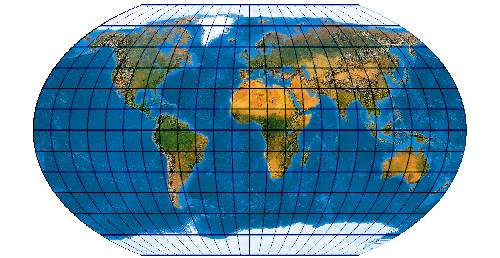
[Evenden 2004: 6.2.7]
(McBryde-Thomas Flat-Polar Sinusoidal)
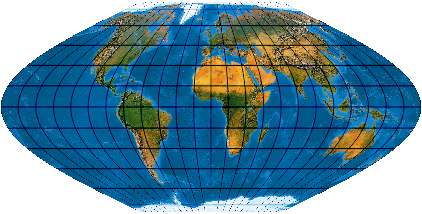
Ähnlich Eckert VI. [Evenden: 6.2.1 (3.)]
(McBryde-Thomas Flat-Polar Parabolic)
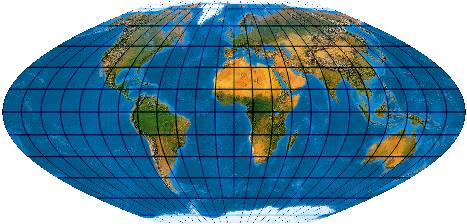
[Evenden 2004: 6.2.19, Evenden 2005: 5.2.25]
(McBryde-Thomas Flat-Polar Quartic)
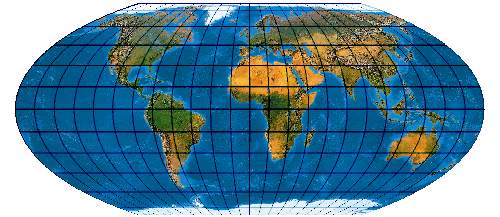
[Evenden 2005: 5.2.27]
(McBryde-Thomas Flat-Polar Sine No. 1)
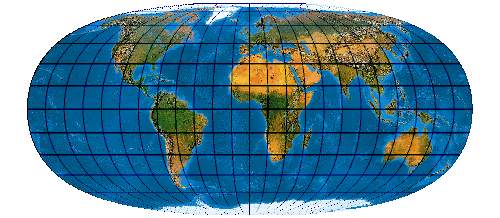
[Evenden 2005: 5.2.26]
(McBryde-Thomas Sine)
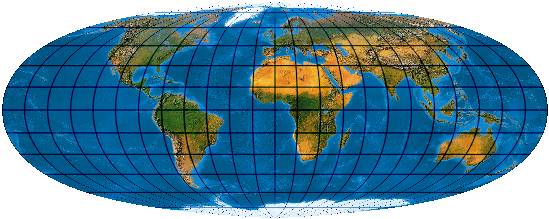
Das „Sine“ bezieht sich auf die Parallelkreisfunktion, nicht auf die Meridianform. [Evenden: 6.2.23 (3.)]
Hinter den 12 Putnins-Netzen steckt System. Es gibt immer eine Hauptvariante mit dem Pol als Punkt und eine Apostroph-Variante mit Pollinie.
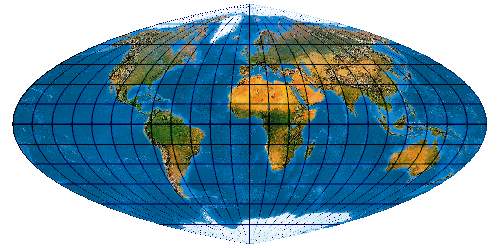
[Evenden 2005: 5.2.7]
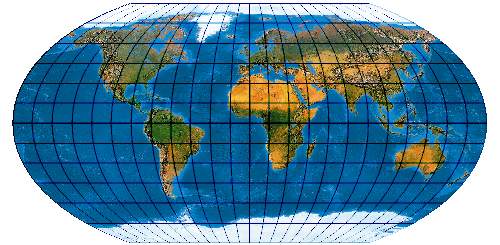
[Evenden 2005: 5.2.7]
[Evenden 2005: 5.2.18]
[Evenden 2005: 5.2.14]
Der Putnins P'2 entspricht dem Wagner IV.
[Evenden 2005: 5.2.19]
[Evenden 2005: 5.2.19]
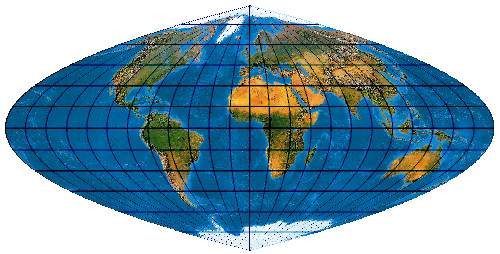
[Evenden 2005: 5.2.17]
Der Putnins P4 entspricht dem Craster.
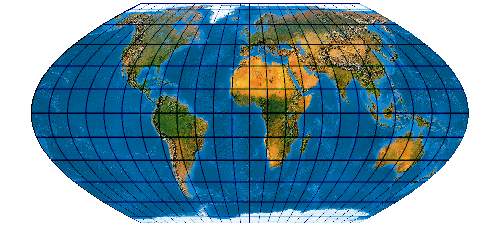
[Evenden 2005: 5.2.20]
Der P'4 ähnelt dem Werenskiold I.
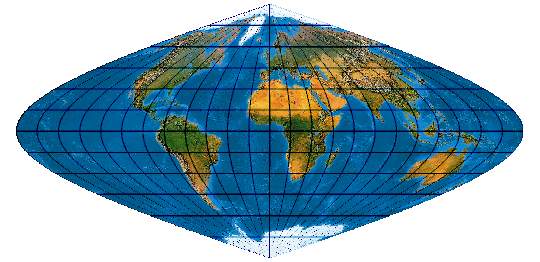
[Evenden 2005: 5.2.21]
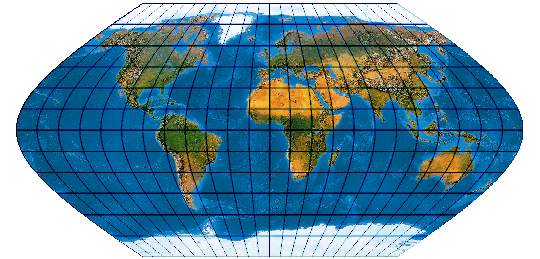
[Evenden 2005: 5.2.21]
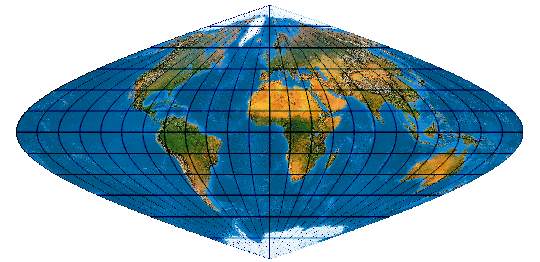
[Evenden 2005: 5.2.21]
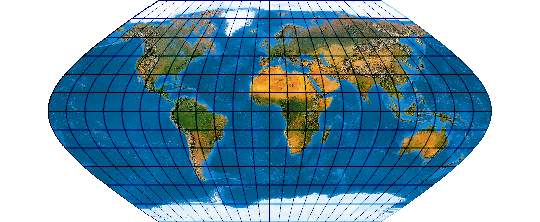
[Evenden 2005: 5.2.21]
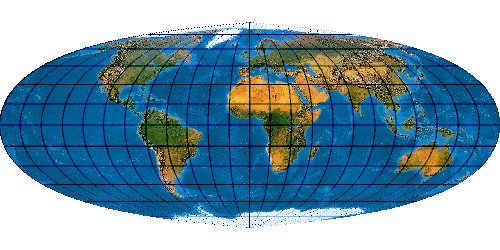
Toblers hat in seinem Aufsatz „The Hyperelliptical and Other New Pseudo Cylindrical Equal Area Map Projections“ eine Reihe von flächentreuen Pseudozylindern unter „Hyperellipticals“ gleichsam zusammengefasst und generalisiert. Fig. 1. (des Aufsatzes) zeigt einen Foucaut aus dem Jahr 1862 (nicht mit den Foucaut der Evendenschen Sine-Tangent-Series zu verwechseln), Fig. 2 den Nell-Hammer, Fig. 3 den Tobler G1.
[Tobler 1973: The Hyperelliptical and Other New Pseudo Cylindrical Equal Area Map Projections. Journal of Geophys. Research, Vol. 78, No. 11, Apr. 10, 1973]
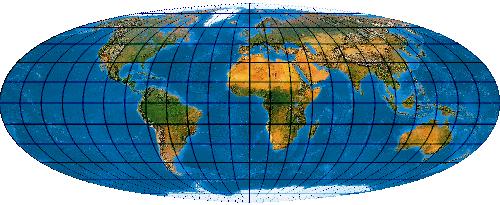
[Evenden 2005: 5.2.50]
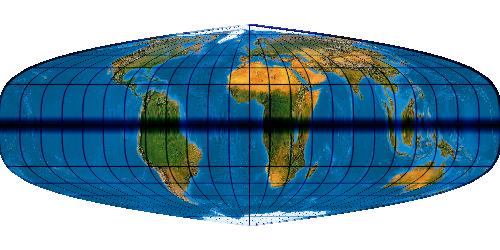
[1986: Polycylindrical Map Projections. The Americal Cartographer, Vol. 13, No. 2, pp. 117-120, Figure 5/1]

[1986: Polycylindrical Map Projections. The Americal Cartographer, Vol. 13, No. 2, pp. 117-120, Figure 5/2]
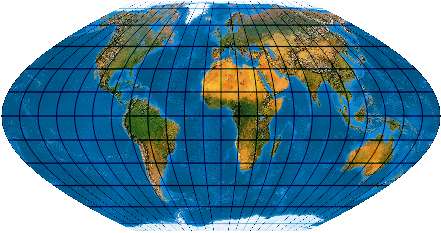
Die Pollinienlänge ist einstellbar und beträgt in der Abbildung 40 % der Äquatorlänge. [Evenden: 6.2.2]
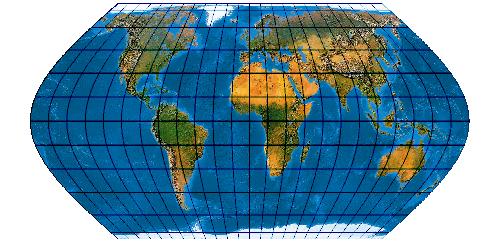
[Evenden 2005: 5.2.36]
Werendskiold Pseudozylinder gehören zu den klassischen Polliniennetzen, die in großer Anzahl in der ersten Hälfte des 20. Jahrhunderts entwickelt wurden. Sie zeichnen sich durch eine besondere Harmonie aus und wurden deshalb in der Literatur gern zitiert.
Der Werenskiold I ist mit dem Putnins P'4 identisch.
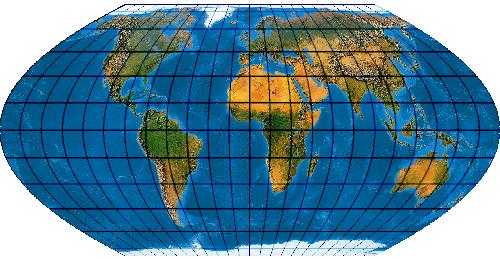
[Evenden 2005: 5.2.20]
Der Werenskiold II ähnelt dem Wagner I.
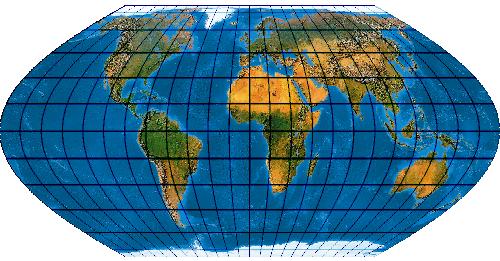
[Evenden 2005: 5.2.4]
Der Werenskiold III ist ein Verwandter des Wagner IV.
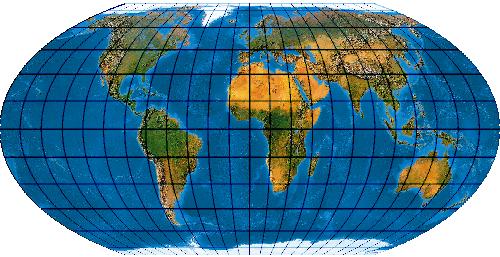
[Evenden 2005: 5.2.14]
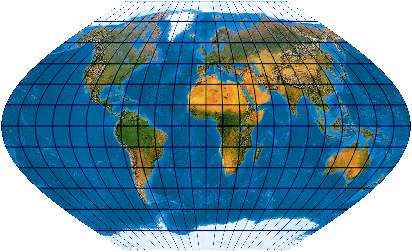
[Evenden: 6.2.4]
Der Winkel I ist weniger verbreitet, als sein berühmter Bruder Winkel III (der Winkel Tripel). Dieser hat allerdings gekrümmte Parallelkreise und ist deswegen kein Pseudozylinder.

Der Winkel II, wie sein „Bruder“ Winkel I ein Pseudozylinder, ist der unbekannteste Vertreter aus dem Hause Oswald Winkel. Weil er kaum in Karten noch in Netzentwurfs-Lehrbücher Eingang gefunden hat, hier einmal ein kleines Zitat im Webspace.
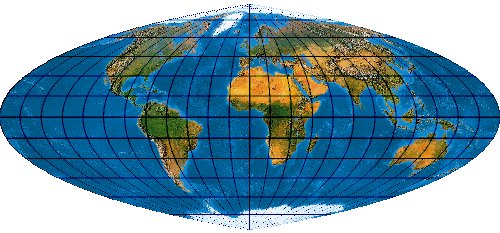
Siehe M. Márton: Die kartographische Darstellung der Ozeane in der geänderten Projektion IV. von Baranyi, Kartographische Nachrichten, 3/2006, S. 145ff.
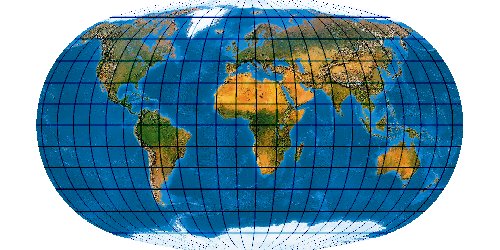
M. Márton: Die kartographische Darstellung der Ozeane in der geänderten Projektion IV. von Baranyi, Kartographische Nachrichten 3/2006, S. 145ff.
Ein speziell für die Abbildung der Ozene geschaffenes Netz. Der Entwurf muss mit einer „Quell-Erd-Plattkarte“, die von -100° bis 300° reicht, gerechnet werden.
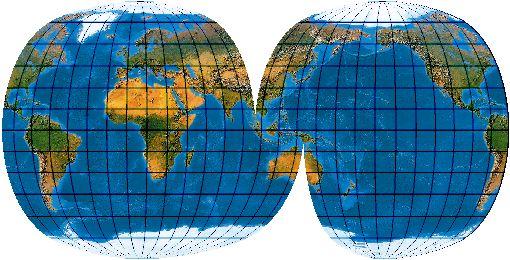
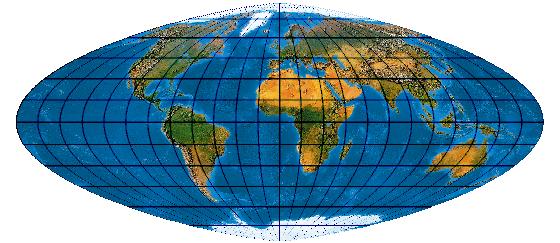
[Evenden 2005: 5.2.28]
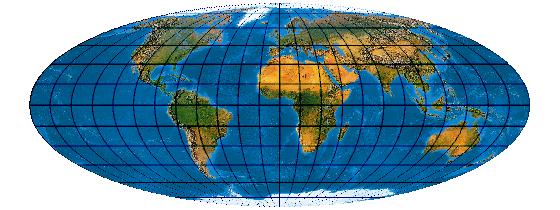
[Evenden 2005: 5.2.14]
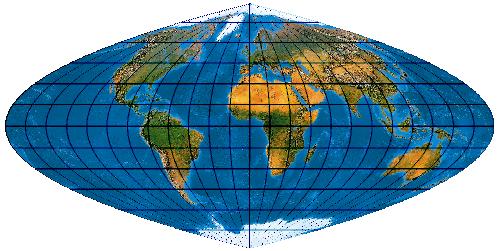
[Evenden 2005: 5.2.17]
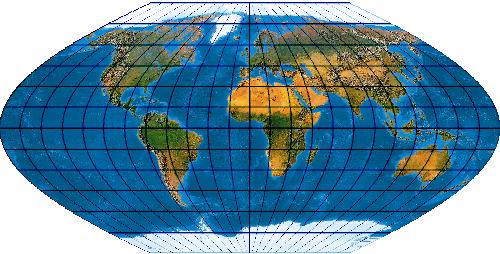
[Evenden 2005 5.2.32]
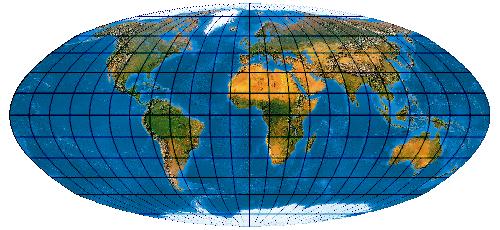
[Evenden 2005: 5.2.41]
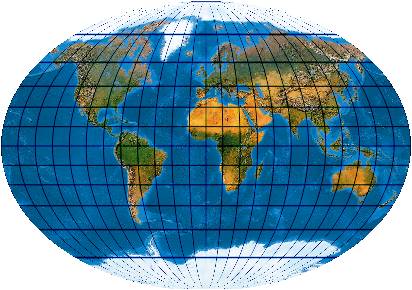
[Evenden 2004: 6.2.33]
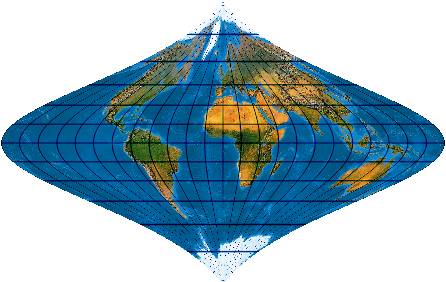
Ein „Tangent series“-Entwurf. [Evenden 2004: 6.2.23 (1.)]
Ein gewichtetes Mittel aus abstandstreuem Zylinderentwurf (quadratischer Plattkarte) und Mercator-Sanson. Es handelt sich im Prinzip um den Tobler-Foucaut (1862), allerdings ist bei jenem das Mischungsverhältnis mit 50:50 fest und hier variabel. Hier einmal eine Mischung mit 75 % Mercator-Sanson
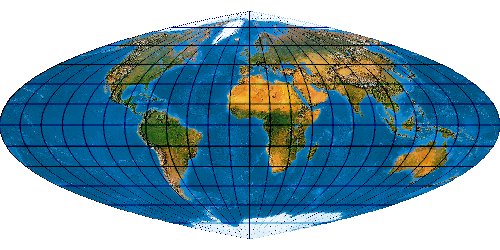
[Evenden 2005: 5.2.13]
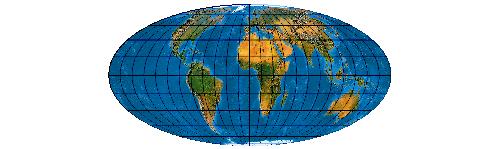
[Evenden 2005: 5.2.48]
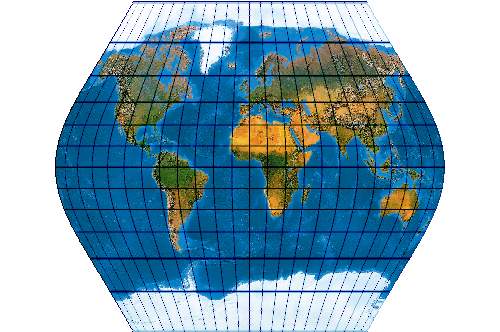
[Evenden 2005: 5.2.34]
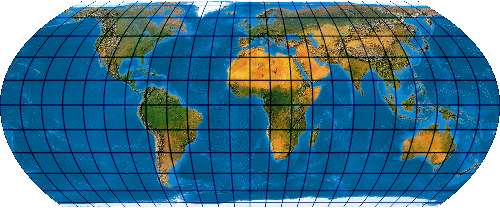
[Evenden 2004: 6.2.12]
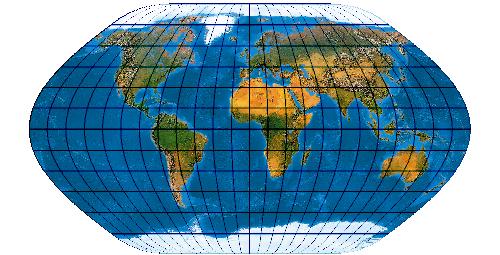
[Evenden 2005: 5.2.15]
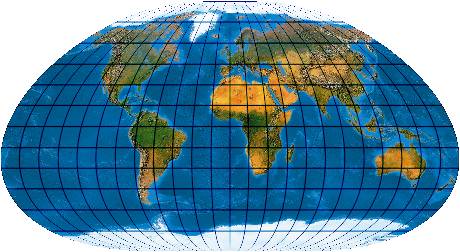
Alle Loxodromen, die durch den Kartenmittelpunkt gehen (In der Abbildung 45° N) werden (wie in der Merkatorprojektion) als Geraden abgebildet, zusätzlich aber auch noch längentreu. Loxodromen sind Linien, die alle Parallelkreise unter demselben Winkel schneiden. Auf der Erdoberfläche handelt es sich um logarithmische Spiralen um die Pole.[Evenden: 6.2.33]
[Evenden 2005: 5.2.35]
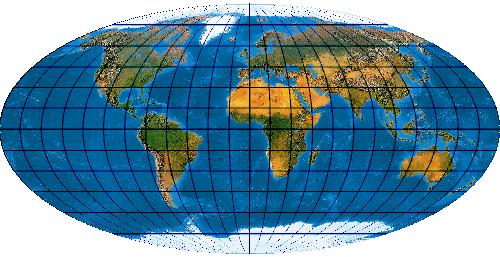
[Evenden 2005: 5.2.38]
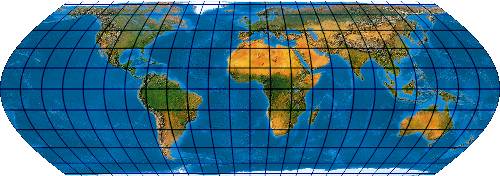
[Evenden 2004: 6.2.27]
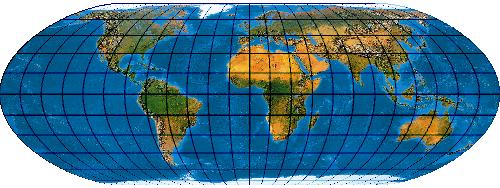
[Evenden 2005: 5.2.30]
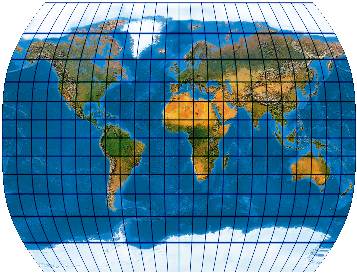
[Evenden 2005: 5.2.46]
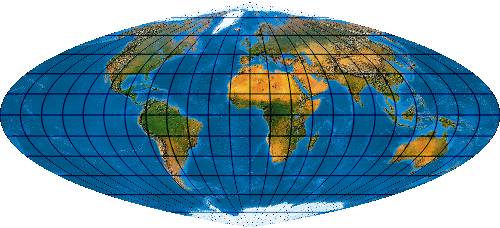
[Evenden 2004: 6.2.23 (2.)]
![]()
[Evenden 2005: 5.2.40]
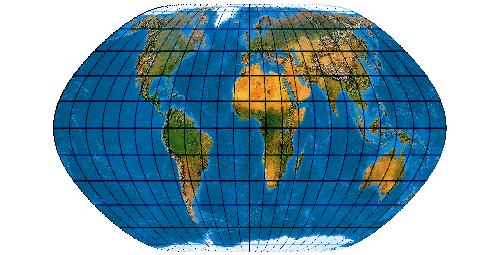
[Evenden 2005: 5.2.42]
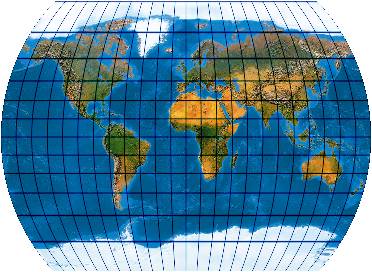
[Evenden 2005: 5.2.46]
Assemblerprogramme:
Canters Low Error Pseudocylindric I (Direktprogramm)
Canters Low Error Pseudocylindric II (Direktprogramm)
Canters Low Error Pseudocylindric III (Direktprogramm)
Canters Low Error Pseudocylindric IV (Direktprogramm)
Eckert I
Eckert II
Eckert III
Eckert IV
Eckert V
Eckert VI
Eckert-Greiffendorf (Direktprogramm)
[Eckert IV:] Wagner Y1 (Eckert IV-Adaption, authentisch) (Direktprogramm)
[Eckert IV:] Wagner Y2 (Eckert IV-Adaption mit 2 längentreuen Parallelkreisen) (Direktprogramm)
Eckert-Furuti
Kavraiskiy V
Kavraiskiy VI (Direktprogramm)
Kavraiskiy VII (Direktprogramm)
McBryde-Thomas-Entwurf mit parabolischen Meridianen und Pollinie
McBryde-Thomas-Entwurf mit quartischen Meridianen und Pollinie (Direktprogramnm)
McBryde-Thomas-Sinusentwurf Nr. 1 mit Pollinie (Direktprogramm)
McBryde-Thomas-Sinusentwurf mit Pol als Punkt
Putnins P1 (Direktprogramm)
Putnins P'1 (Direktprogramm)
Putnins P2 (Direktprogramm)
Putnins P'2 (Direktprogramm)
Putnins P3 (Direktprogramm)
Putnins P'3 (Direktprogramm)
Putnins P4 (Direktprogramm)
Putnins P'4 (Direktprogramm)
Putnins P5 (Direktprogramm)
Putnins P'5 (Direktprogramm)
Putnins P6 (Direktprogramm)
Putnins P'6 (Direktprogramm)
Tobler Foucaut 1862 (Direktprogramm)
Tobler G1 (Direktprogramm)
Tobler Polycylindrical (1986) Fig. 5/1 (Direktprogramm)
Tobler Polycylindrical (1986) Fig. 5/2 (Direktprogramm)
Urmayevs sinusoidaler Entwurf mit Pollinie
Urmayev V (Direktprogramm)
Werenskiold I (Direktprogramm)
Werenskiold II (Direktprogramm)
Werenskiold III (Direktprogramm)
Adams Orthembadic (Direktprogramm)
Baranyi IV (Direktprogramm)
Baranyi-Márton (Direktprogramm)
Boggs Eumorphic (Direktprogramm)
Bromley (Direktprogramm)
Craster (Direktprogramm)
Denoyer (Direktprogramm)
Érdi Krausz (Direktprogramm)
Fahey
Foucaut
Foucaut Sinusoidal (Direktprogramm)
Fourtier II (Direktprogramm)
Ginzburg VIII (Direktprogramm)
Hatano
Hölzel (Direktprogramm)
Loxodromentreuer Entwurf
Mollweide Equidistent (Direktprogramm)
Nell
Nell-Hammer (Direktprogramm)
Oxford Atlas
Quartic Authalic
Semiconformal (Direktprogramm)
Snyder Minimum Error (Direktprogramm)
Times Atlas
Durchsicht 08.10.2014.