Verzeichnis aller Canters-Netze. Canters Index Table with all projections
[Canters Projections of the European Union]
Um die Länder der Europäischen Union optimal abzubilden, wird zunächst ein schief gelagerter flächentreuer (Lambertscher) Azimutalentwurf gerechnet ...
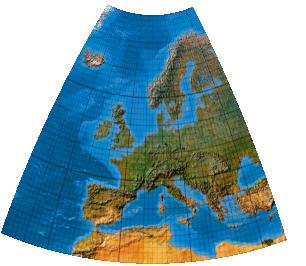
Nun wird dieses Netz mit einer ebenen x-y-zu-x'-y'-Transformation erneut abgebildet. Dabei werden spezielle von Canters entwickelte Polynome zum Einsatz kommen, die die Flächentreue erhalten. Es handelt sich also nicht um Projektionen der üblichen Art (Erde in Karte), sondern um sog. Post-Transformationen einer bereits vorliegenden Karte (Karte in Karte). Außerdem wird bei Canters EU-Entwürfen die Kartenebene vor der Post-Transformation um einen Winkel Θ verdreht.
First-order low-error transformation
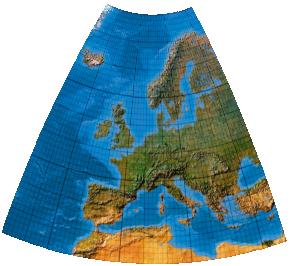
Das Kartengebiet reicht von 25°W bis 35°E. Dadurch befindet sich der rechnerische Mittelmeridian 7° allerdings nun 32° vom Westrand, aber nur 28° vom Ostrand entfernt. Die im Osten fehlenden 4 Grad, wurden, um Canters authentisch zu wahren, bewusst nicht ergänzt. So ergibt sich die etwas assymetrische Kartenaußenform.
[Canters (2002), p. 243f., Tab. 5.26, Fig. 5.43]
Second-order one-fold symmetric low-error transformation for the European Union
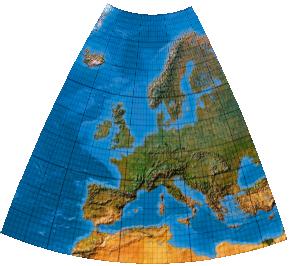
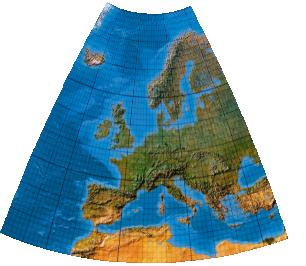
Polynome zweiten Grades mit einer Symmetrieachse.
Weil sich die optimierten Europakarten nur ganz gering unterschieden, wird neben der Abbildung links, die das richtige Bild zeigt, rechts ein Bild mit dreifach verstärkten Koeffizienten gezeigt.
Left image: Correct computation. Right Image: computation with threefold coefficients as illustration.
[Canters (2002), p. 243f., Tab. 5.26, Fig. 5.44]
Second-order transformation without symmetry
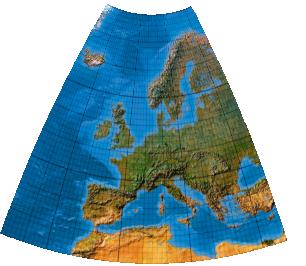
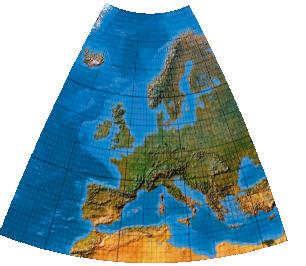
Polynome zweiten Grades ohne Symmetrie
[Canters (2002), p. 243f., Tab. 5.26, Fig. 5.46]
Second-order transformation without symmetry (single boundary definition)
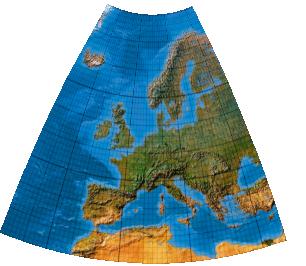
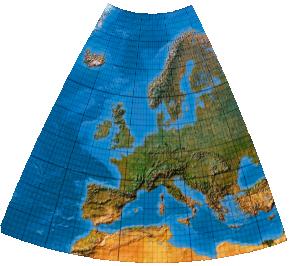
Wie P32, jedoch EU-Begrenzung durch eine gesondert definierte Grenzlinie, die auch Nordsee, Golf von Biscaya und küstennahe Meeresflächen in die Optimierung einbezieht.
[Canters (2002), p. 243f., Tab. 5.28, Fig. 5.50]
Third-order one-fold symmetric low-error transformation for the European Union
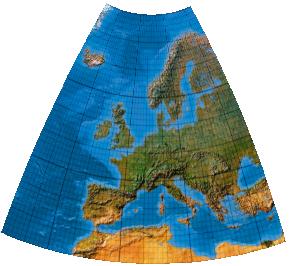
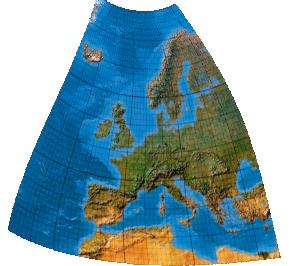
Nun mit kubischen Polynomen. Version mit einer Symmetrieachse.
[Canters (2002), p. 243f., Tab. 5.26, Fig. 5.45]
Third-order transformation without symmetry
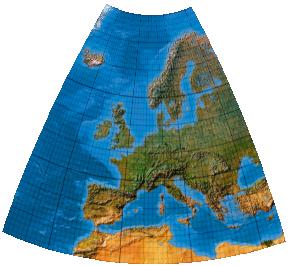
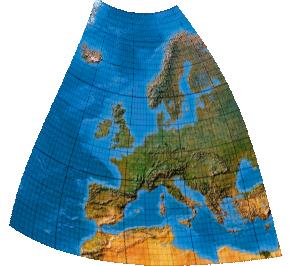
Kubische Polynome. Version ohne Symmetrieachse.
[Canters (2002), p. 243f., Tab. 5.26, Fig. 5.47]
Third-order transformation without symmetry (single boundary definition)
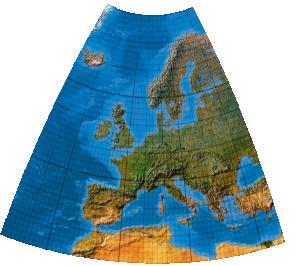
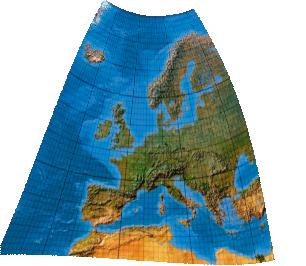
Kubische Polynome. Version ohne Symmetrieachse und mit gesondert definierter Umgrenzungslinie
[Canters (2002), p. 243f., Tab. 5.28, Fig. 5.51]
Fifth-order one-fold symmetric low-error transformation for the European Union
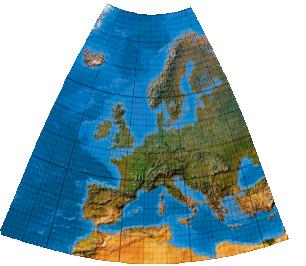
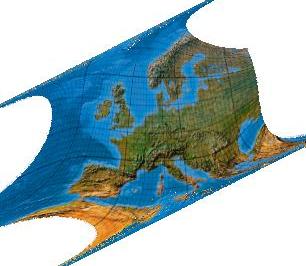
Polynome 5. Grades. Version mit einer Symmetrieachse.
[Canters (2002), p. 243f., Tab. 5.26, no Fig.]
Third-order transformation without symmetry
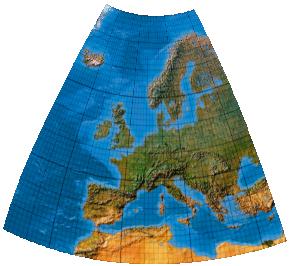
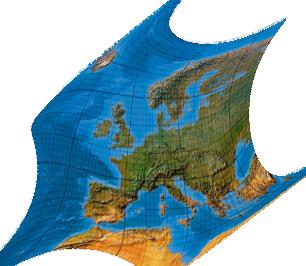
Polynome 5. Grades. Version ohne Symmetrieachse.
[Canters (2002), p. 243f., Tab. 5.26, Fig. 5.48]
Third-order transformation without symmetry (single boundary definition)
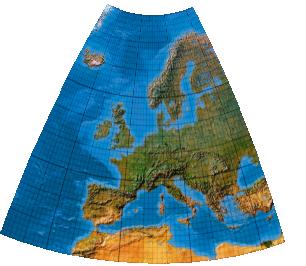
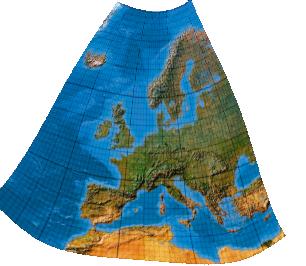
Polynome 5. Grades. Version ohne Symmetrieachse mit spezieller Umgrenzungslinie
[Canters (2002), p. 243f., Tab. 5.28, Fig. 5.52]
Die Europa-Bilder dieser Seite haben den Maßstab 1:200.000.000 (bei 254 dpi).
Bei Rechnen mit Vimage ist zu beachten: Zuerst ist der schiefachsige flächentreue Azimutalentwurf Erdkugel auf Kartenebene zu rechnen. Die eigentlichen Programme rechnen nur eine sog. Post-Projektion, die den Azimutalentwurf erneut transformieren. Hier die Programme:
1. Stufe (Erdkugel auf Kartenebene)
Schiefachsiger flächentreuer Azimutalentwurf (Programm)
Schiefachsiger flächentreuer Azimutalentwurf (Direktprogramm, Snyders Formel, etwas schneller)
2. Stufe (Post-Transformation Karte auf Karte)
Die Programme führen auch die Verdrehung der Karte um den Winkel Θ aus, die Canters vor der Transformation anweist. Nach der Transformation wird die Karte um diesen Winkel zurückgedreht.
Weil die Polynome auf dem Einheitskugelradius als Einheit aufbauen, fragen die Post-Projektionsprogramme erneut eine Maßstaszahl ab (obwohl der Maßstab ja schon in der 1. Stufe gerechnet wurde). Diese muss bei beiden Transformationen identisch angegeben werden.
Canters Low-error Projection (EU) P30 (Direktprogramm)
Canters Low-error Projection (EU) P31 (Direktprogramm)
Canters Low-error Projection (EU) P32 (Direktprogramm)
Canters Low-error Projection (EU) P33 (Direktprogramm)
Canters Low-error Projection (EU) P34 (Direktprogramm)
Canters Low-error Projection (EU) P35 (Direktprogramm)
Canters Low-error Projection (EU) P36 (Direktprogramm)
Canters Low-error Projection (EU) P37 (Direktprogramm)
Canters Low-error Projection (EU) P38 (Direktprogramm)
Canters Low-error Projection (EU) P39 (Direktprogramm)