Der Pol wird an besten auf eine Ebene abgebildet.
Die Äquatorialgegend kann man leicht auf einen Zylinder projizieren.
Und die Gebiete dazwischen? Wenn man nun zwischen Äquator und Pol (unendlich) viele kegelige Körper anordnet, die man allmählich von Zylinder über spitze Kegel und flachere Kegel bis in die Ebene deformiert und auf jeden dieser Körper jeweils einen (unendlich dünnen) Parallelkreis abbildet — müsste das dann nicht ein Kartenentzentwurf gelingen, in welchem jede Erdgegend sehr vorteilhaft abgebildet wird?
Diesen Gedanken hatte zuerst F. R. Hassler, der erste Direktor des U. S. Coast Survey im Jahr 1820.
Auf Greenwich zentriert. Centered on Greenwich Meridian:
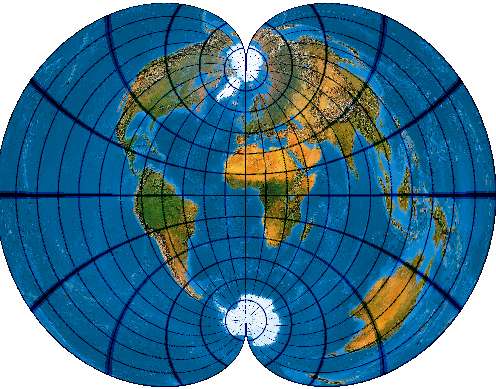
Und hier Carlos A. Furutis, auf -100 Grad zentrierte Version. And here the Carlos A. Furutis Version, Central Meridian 100 ° West:
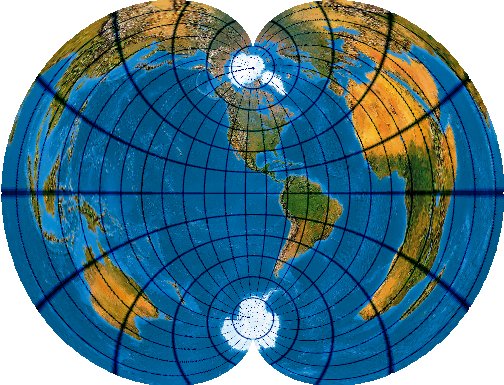
Auf Greenwich zentriert. Centered on Greenwich Meridian:
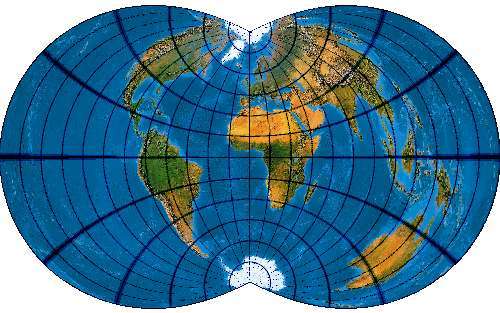
Auch hier Carlos A. Furutis, auf -100 Grad zentrierte Version. Here also the Carlos A. Furutis Version, Central Meridian 100 ° West:
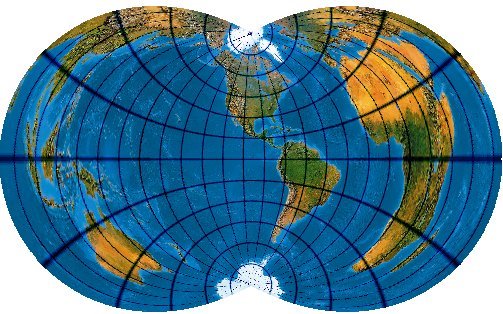
Auf Carlos A. Furutis Webseite fand ich eine generalized, transverse polyconic projection, die mich faszinierte. Die musste ich haben! On Carlos A. Furutis Webpage I found a generalized, transverse polyconic projection. What a famous Earth image! That I must have in my collection.
Was macht Furuti mit Old Hassler von Coast und Geodetic Survey? What is the kernel of Furutis idea?
Zuerst bringt es die Erde in eine transversale Lage, d. h. er dreht er die Erdpole innerhalb der Kugeloberfläche auf den Äquator. Lage des Meta-Poles bei 0° N, 95° E, weiterhin erfolgt eine Post-Transformation-Rotation um ebenfalls 95° Länge. First he rotates the earth poles into the equator. Meta pole position 0° N, 95° E, post transformation longitude rotation also 95°.
Dies hat mit der eigentlichen Projektion noch nichts zu tun und erfolgt als sog. Meta- oder Protoabbildung vor der Projektion. Hierbei wird die Erde auf sich selbst abgebildet. Note: That is a pre-projection meta transformation earth sphere into earth sphere.
 Transversaler abstandsgleicher polykonischen Entwurf.
Transversaler abstandsgleicher polykonischen Entwurf.
Dann wird ein konstanter „Assymetric Shift“-Winkel λAS eingeführt. Diesen setze man in der Netzentwurfs-Lehrbuchformel α=sin(φ)*λ ein mit α=sin(φ)*(λ+λAS). Than change the common projection formula α=sin(φ)*λ into α=sin(φ)*(λ+λAS), where λAS is a constant „asymetric shift angle“
Nun wird der abstandsgleiche polykonische Entwurf mit Nullmeridian λ0=-25° und λAS=-30° gerechnet. Then compute the polyconic with central meridian λ0=-25° and λAS=-30°:
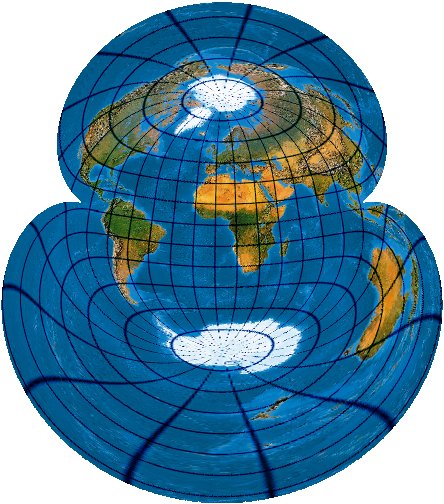
Wenn man die Parameter etwas anders wählt, wird der Äquator zum Aussenrand und es ergibt sich ein noch schöneres Erdbild. Here my own version with the equator as map border:
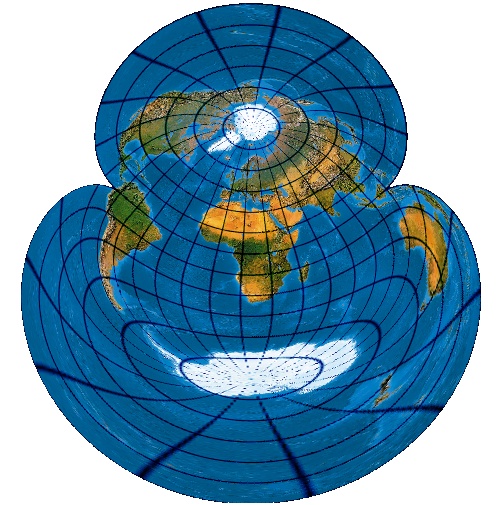
Erdrotationsparameter: Metapol 0° N, 110° E, Post-Rotation um 110°. Projektionsparameter: λ0=-20° und λAS=-40°
Earth rotation into meta pole 0° N, 110° E, longitudenal post rotation 110°. Projection: λ0=-20° und λAS=-40°
Hier die Karte im Großformat Here the map in high resolution: (600 kByte)
Die ungarischen Kartographen J. Györffy und I. Klinghammer haben ein Netz gesucht, das Europa mit den geringst möglichen Verzerrungen abbildet, und sind in der Gruppe der „Pseudopolyconicals“ fündig geworden. In den Kartographischen Nachrichten Nr. 6/2004 stellen sie das Ergebnis vor. Hier eine Seite mit den Györffy-Netzen
Assemblerprogramme:
(Die Programme der polykonischen Entwürfe sind Direkttransformationsprogramme)
Abstandstreuer polykonischer Entwurf
Orthogonaler polykonischer Entwurf
Orthogonaler polykonischer Entwurf, Furutis Verallgemeinerung